Для удобства инженеров в программном комплексе midas Civil существует разделение рассчитываемых элементов на балки и колонны. В данной статье мы не будем углубляться в предпосылки такого разделения, а примем как факт то, что балки рассчитываются как изгибаемый элемент, а колонны — как сжатый или внецентренно сжатый. Как известно, сталкиваясь с задачей по расчету сжатых элементов, инженеры не так часто имеют дело с чистым сжатием. Например, при расчете стоек опор недостаточно учитывать только продольную силу, а следует также учитывать момент, который возникает из-за случайного эксцентриситета вертикальной нагрузки, а также в целом моменты от действующих нагрузок. Таким образом, колонны подвержены комбинированному воздействию усилий, что, в свою очередь, может приводить к трудностям при прогнозировании их разрушения. В данной статье рассмотрим такой инструмент как кривая взаимодействия Р-М, которая достаточно точно помогает описать сложное воздействие усилий на колонну, а также покажем, как в этом может помочь midas Civil.

Зачем нужна кривая Р-М?

Основная суть кривой Р-М — это графическое представление расчетной прочности нагруженной колонны. Важно отметить, что различные осевые нагрузки приводят к разным моментам разрушения. Но при использовании кривой взаимодействия можно быстро сделать вывод — проходит ли данная колонна по несущей способности при известном значении изгибающего момента и продольной силы в сечении.

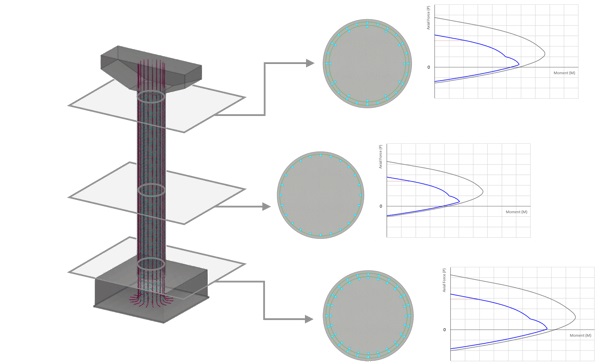
Рисунок 1. Кривые взаимодействия для разных участков стойки опоры

Приведенное ниже уравнение описывает характер взаимосвязи между продольной силой и изгибающим моментом при достижении предела прочности.

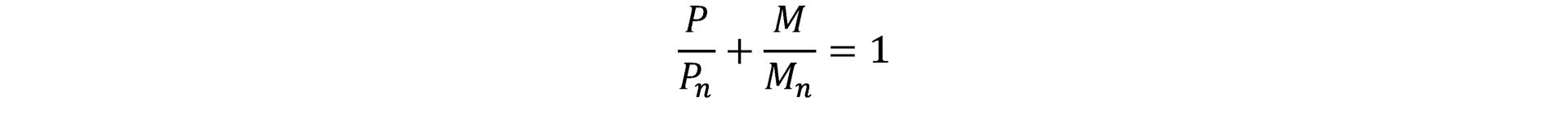
В данной формуле:

• P — действующая продольная сила;
• М — действующий изгибающий момент;
• Pn — предельная продольная сила;
• Mn — предельный изгибающий момент.

Построение кривой взаимодействия для ЖБ колонн

Несмотря на то, что приведенное выше уравнение кажется довольно простым, процесс вычисления предельных усилий в зависимости от действующих нагрузок довольно трудоемкий. Из-за этого кривые взаимодействия рассчитываются исходя из предположения о множестве распределений деформаций, каждое из которых соответствует определенной точке на кривой взаимодействия, а уже затем определяются соответствующие значения Pn и Mn. Такой метод позволяет вычислить достаточное количество точек, из которых и формируется кривая взаимодействия Р-М.

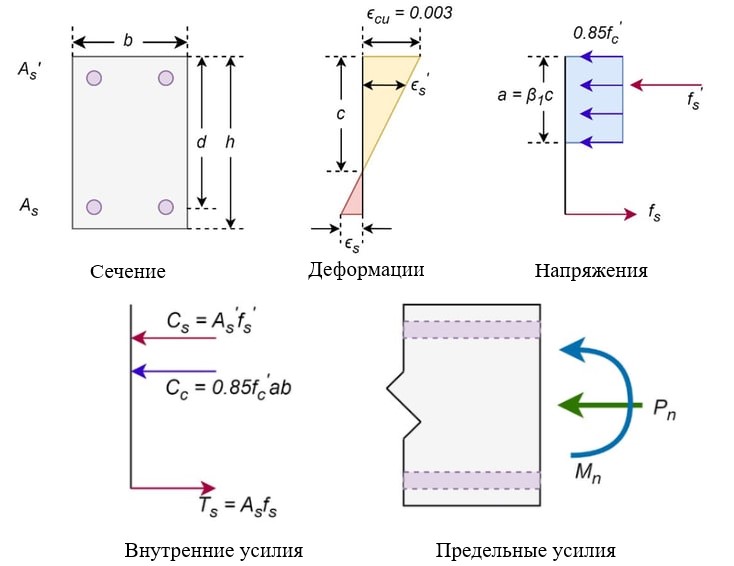
Рисунок 2. Схема распределения напряжений и деформаций в ЖБ колонне

На рисунке выше показана схема расчета для одного распределения деформаций. Деформация на каждом уровне армирования получается из кривой распределения деформации при определенном положении нейтральной оси. Напряжения в свою очередь вычисляются исходя из получаемых значений деформаций. Силы в бетоне и в арматуре вычисляются путем умножения значений напряжений на площади, в рамках которых возникают данные напряжения. Вычисление осевой силы и момента после вышеперечисленных процедур не составляет труда. Другие точки на диаграмме выбираются путем выбора различных значений высоты «с» — расстояния от нейтральной оси до фибры с максимальным сжатием.

Как определить, проходит ли колонна по несущей способности?

Построив кривую взаимодействия Р-М и зная действующие усилия, уже легко можно понять, проходит ли колонна по несущей способности. Для этого достаточно определить лежит ли точка с координатами (М, Р) в зоне, которую ограничивает кривая взаимодействия.

Теперь, имея кривую Р-М и зная действующие усилия для конкретного эксцентриситета, можно получить значения максимального момента и осевой силы, которые можно приложить к колонне. Для этого можно провести линию с наклоном «1:е», пересекающую кривую взаимодействия, то есть, принимая постоянное значение М/Р. Точно также можно определить максимальную нагрузку и эксцентриситет, при котором она может быть приложена. То есть, сохраняя либо значение Р, либо значение М постоянным.

Далее рассмотрим некоторые особенности кривой взаимодействия Р-М.

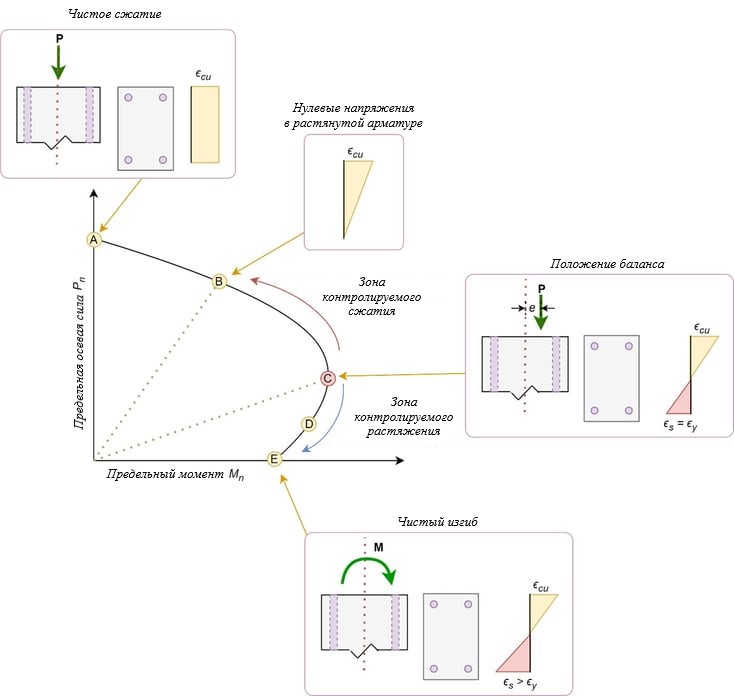
Рисунок 3. Зоны кривой Р-М для колонны при внецентренном сжатии

Точка, А — чистое сжатие, действует только осевая сила. В сечении возникает равномерное сжимающее напряжение от максимальной осевой нагрузки, которую способно выдержать заданное сечение.

Точка В — нулевые растягивающие напряжения, начало трещинообразования в наименее сжатой фибре колонны. Поскольку растягивающие напряжения в бетоне не учитываются при расчете прочности, разрушающие нагрузки ниже точки В на диаграмме представляют собой случаи, когда сечение частично растрескивается.

Зона А-С — зона контролируемого сжатия. Колонны с осевыми нагрузками и моментами, попадающими на верхнюю ветвь кривой взаимодействия между точками, А и С разрушаются из-за смятия сжатой зоны до того, как растянутая арматура достигнет своего предела текучести.

Точка С — точка баланса, сбалансированное разрушение. В данной точке деформации в бетоне достигают максимальной деформации сжатия, а деформации растяжения в арматуре, наиболее удаленной от сжатой грани, равна деформации текучести. Поэтому в данной точке одновременно происходит разрушение бетона по сжатию и арматуры по растяжению.

Точка D — предел контролируемого растяжения. В данной точке происходит пластическое разрушение. Зона С-D — переходная область. Характер разрушения в данной зоне формируется в виде перехода от хрупкого разрушения к пластическому.

Реализация построения кривой в midas

Представим расчет кривой взаимодействия для сжатой колонны произвольного с учетом изгиба в двух плоскостях. Задача будет очень трудоемкой, даже с использованием собственных средств автоматизации. Здесь в помощь инженерам подключается midas. При проверках сечений ЖБ колонн программа сгенерирует кривую Р-М, также можно воспользоваться модулем GSD, который позволит построить данные кривые уже для более сложных задач. Подробнее о модуле GSD вы можете прочитать в статье:

• Читайте статью: Применение модуля GSD: проектировщик сечений

.

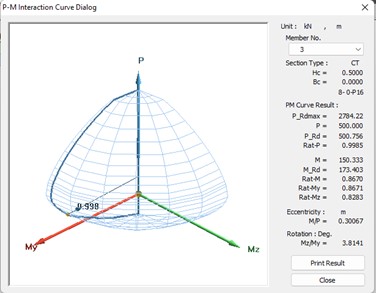
Рисунок 4. Кривая Р-М в модуле проверок ЖБ колонн

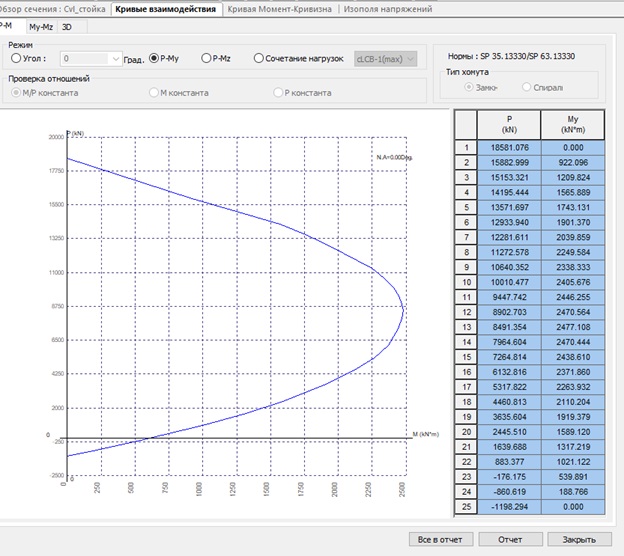
Рисунок 5. Кривая Р-М в модуле GSD

Спасибо, что прочитали данный материал до конца. Мы, команда технической поддержки, надеемся, что данная статья будет для вас полезной в вашей трудовой деятельности.