Геометрические свойства сечений являются показателями конструктивных характеристик и несущей способности сечений. Они нужны для расчета прочности, устойчивости, изгибных и сдвиговых напряжений, прогибов — важных факторов в процессе общего проектирования конструкций мостов. Характеризуются формой и размерами сечений независимо от свойств материала.

В этой статье мы рассмотрим, как можно вычислить эти свойства сечений самостоятельно «в ручном режиме». В конце статьи вы можете скачать два калькулятора свойств двутаврового и коробчатого сечений в формате Excel для самостоятельного использования. А если вы хотите полностью избежать утомительной работы и сэкономить время, избежать повторяющихся задач и рутины — используйте программный комплекс midas Civil. В нем свойства сечений вычисляются автоматически.

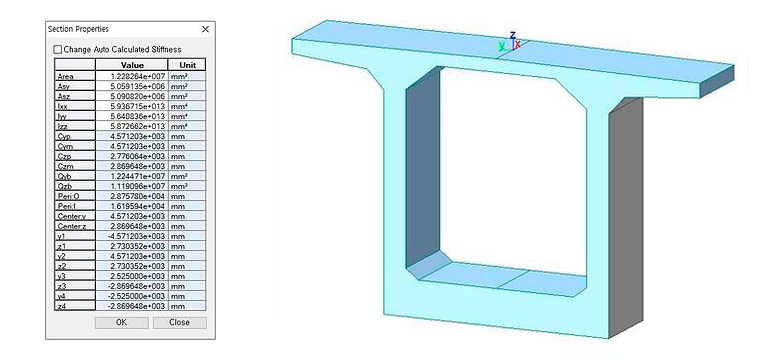
Рисунок 1. Свойства коробчатого сечения, которые вычисляются в midas Civil

Давайте рассмотрим среди свойств сечения соотношение между центром тяжести сечения, статическим моментом площади сечения и моментом инерции, применяемым в формулах изгибных и сдвиговых напряжений, и то, как эти величины можно вычислить.

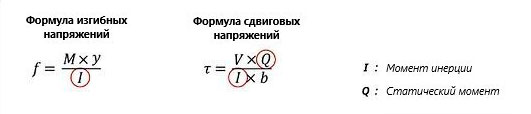
Статический момент площади сечения и центр тяжести

Статический момент площади используется для расчета центра тяжести сечений и касательного напряжения балочных элементов.

• Формулу можно получить следующим образом:
  Линейная область, удовлетворяющая закону Гука, подтверждается при помощи диаграммы отношения между напряжением и деформацией. Отношение между напряжением и деформацией материала с линейным упругим поведением может быть выражено наряду с соотношением между деформацией и кривизной.

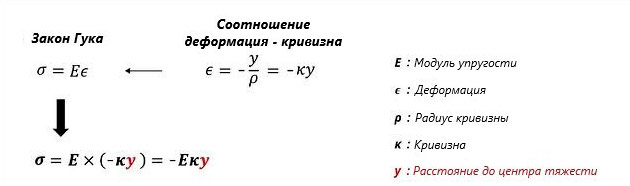
Применив указанное выражение к сечению, в котором действует только изгиб без осевых усилий, как показано на изображении ниже, можно получить выражение, которым вычисляют статический момент площади сечения. Таким образом, сумма нормальных напряжений равна нулю, поскольку действует только изгиб без осевых усилий.

Напряжение «σ1», которое действует на элемент, расположенный на расстоянии «y» от нейтральной оси, и бесконечно малую площадь «dA» в пределах сечения, можно вычислить через выражение, приведенное выше. Сумма напряжений, которые действуют на n-бесконечно малые площади, распределенные по всему сечению, равна 0 и может быть выражена следующим образом. Поскольку кривизна и модуль упругости «E» являются ненулевыми константами, интеграл произведения «dA» и «y» должен быть равен 0.

Из приведенного расчета можно понять, что в случае использования линейно-упругих материалов нейтральная ось становится центром тяжести поперечного сечения; при этом статический момент площади сечения по отношению к центру тяжести сечения равен 0.

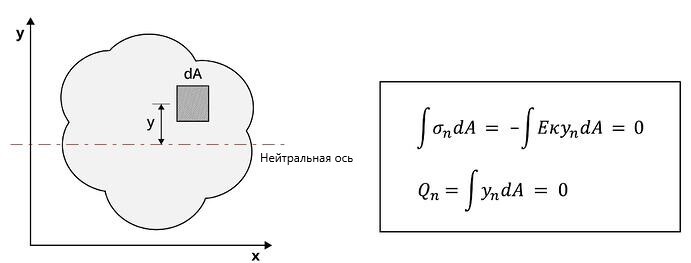
Рисунок 2. Выведение формулы статического момента площади сечения

С помощью показанного на Рисунке 2 выражения можно вычислить статический момент площади сечения и расположение центра тяжести поперечного сечения для тех случаев, когда ось «x» выступает в качестве их базисной оси.

Примеры вычисления статического момента площади

Пример 1

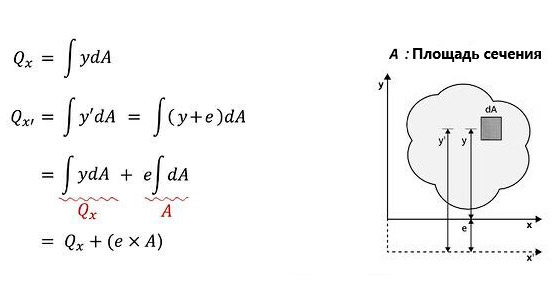
• Вычислив статический момент площади сечения относительно оси «x'», которая расположена на расстоянии «e» от координатной оси «x». Из полученных результатов можно понять, что по мере увеличения расстояния от координатной оси статический момент площади сечения увеличивается на величину «e».
• Расстояние «y'» — расстояние от оси «x'» до соответствующего элемента, можно учитывать отдельно как «y» и «e».

Пример 2

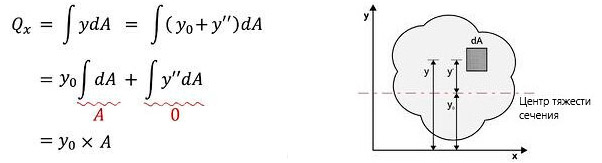
• В этом примере ось «x» задается в качестве базисной оси, и статический момент площади сечения можно вычислить путем вычленения из «y» величин «y0», которая представляет собой расстояние от оси «x» до центра тяжести поперечного сечения, и «y''», которая является расстоянием от центра тяжести поперечного сечения до произвольной области.
• Поскольку статический момент площади сечения от центра тяжести поперечного сечения равен «0», величина «y''» становится «0».
• Таким образом, статический момент площади сечения вычисляется путем умножения общей площади поперечного сечения на значение расстояния от оси «x» до центра тяжести поперечного сечения.
• Следует отметить, что статический момент площади сечения можно вычислить путем умножения общей площади поперечного сечения на расстояние от координатной оси до центра тяжести поперечного сечения.

Пример 3

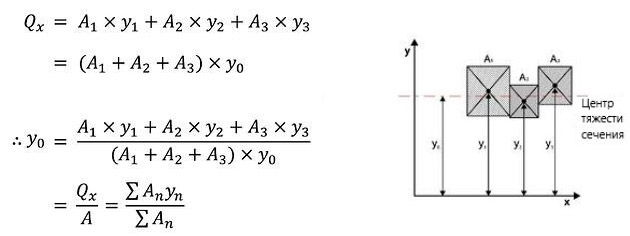
• Статический момент площади сечения можно рассчитать путем сложения произведения площади каждого сечения и расстояния от оси «x» до центра тяжести поперечного сечения.
• Когда известно место расположения центра тяжести поперечного сечения, и когда эти три сечения объединены, статический момент площади сечения можно вычислить как произведение общей площади поперечного сечения и «y0», как показано на примере.
• Из полученного результата можно вывести обобщенное выражение, которое позволит найти центр тяжести поперечного сечения через статический момент площади сечения.

Обобщенную формулу центра тяжести поперечного сечения можно сопоставить с результатами непосредственного расчета центра тяжести поперечного сечения через условия равновесия. Метод расчета расстояния «y0» от координатной оси до центра тяжести поперечного сечения «G» выглядит так:

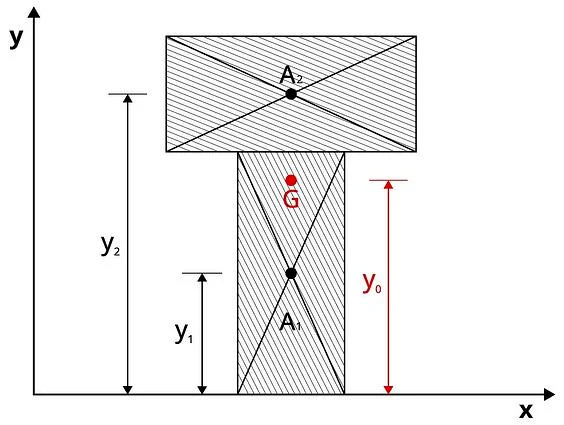
Рисунок 3: Формула центра тяжести поперечного сечения и применение уравнений равновесия

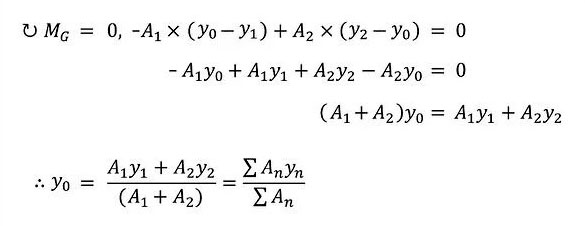
Формула центра тяжести поперечного сечения, полученная через условия равновесия, представляет собой ту же формулу, которая была получена через статический момент площади сечения.

Момент инерции площади поперечного сечения

Момент инерции используется в качестве критерия для определения изгибной жесткости сечения и расчета прогибов, изгибных напряжений и касательных напряжений конструкций. Формулу расчета момента инерции можно получить как соотношение между моментом и кривизной, а также в результате вычисления этого соотношения.

Как показано на Рисунке 4, сумма моментов, создаваемых нормальными напряжениями, которые воздействуют на сечение, равна моменту «M». Эту формулу можно преобразовать в уравнение для напряжения, которое воздействует на сечение, разделенное на n-бесконечно малых элементов. При этом обобщенная формула выглядит так:

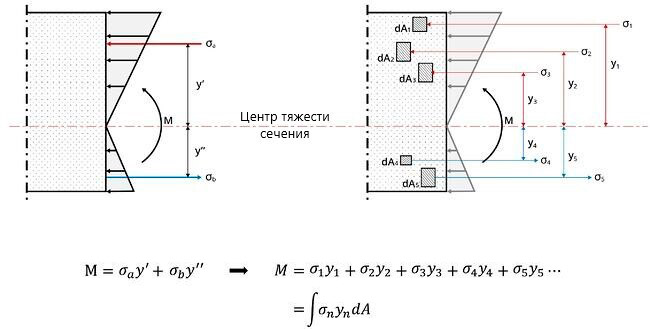
Рисунок 4. Выведение формулы момента инерции

В случае, если полученную выше формулу заменить формулой расчета напряжений линейно-упругого материала, она будет выражена следующим образом: выражение суммы произведения квадрата «y» и площади поперечного сечения называется моментом инерции и обозначается как «I». Поскольку момент инерции является произведением длины в квадрате и площади поперечного сечения, единица выражена как длина в четвертой степени.

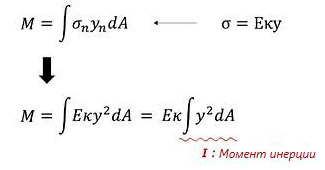
Приведенная выше формула суммируется для кривизны и момента следующим образом: кривизна «κ» пропорциональна моменту и обратно пропорциональна изгибной жесткости «EI». Изгибная жесткость «EI» применяется в качестве стандарта для измерения уровня, на котором элемент конструкции может противостоять изгибу. Благодаря этой формуле можно понять, что модуль упругости и форма, представляющие собой внутренние физические свойства элементов конструкции, являются важными факторами, которые определяют прочность конструкций.

Когда используется материал с большим модулем упругости или поперечное сечение с большим моментом инерции площади, изгибная жесткость увеличивается. С увеличением изгибной жесткости повышается способность конструкции противостоять изгибу, при этом уменьшается ее прогиб, так как угол прогиба или отклонения и момент инерции площади сечения обратно пропорциональны.

Формулу расчета момента инерции площади сечения, полученную указанным способом, можно обобщить на Рисунке 5. Момент инерции площади произвольного сечения при оси «x» в качестве координатной оси рассчитывается следующим образом: расстояние от координатной оси «x» до центра тяжести площади сечения составляет «r», а расстояние от центра тяжести площади сечения до n-бесконечно малых элементов можно подразделить на «y_n».

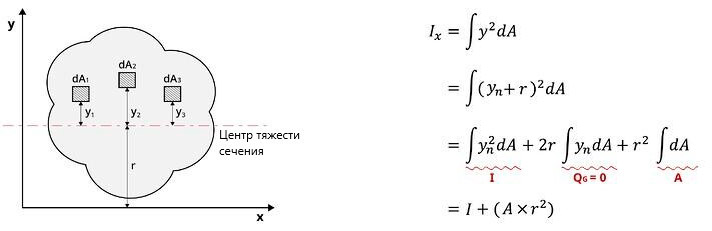
Рисунок 5. Теорема о параллельном переносе осей для момента инерции

Поскольку статический момент площади сечения «Q_G», вычисляемый как интегральное произведение «y_n» и бесконечно малой площади «dA», равен 0, то момент инерции относительно оси «x» можно вычислить как сумму момента инерции «I» и произведение «r²» и площади поперечного сечения «A». Кроме того, площадь поперечного сечения «A» и «r²» всегда являются положительными величинами. Поэтому, когда координатная ось принимается как центр тяжести поперечного сечения, моментом инерции становится наименьшее значение.

Момент инерции обозначен как «I», когда координатной осью является центр тяжести поперечного сечения, и как «I_x», когда координатной осью является ось «x». Из приведенного выше процесса выведения видно, что значение момента инерции варьируется в зависимости от координатной оси. Перемещение координатной оси от центра тяжести поперечного сечения к оси «x» с целью получения обобщенного выражения момента инерции площади сечения сообразно с координатной осью называется теоремой о параллельном переносе осей.

По прямоугольному сечению на Рисунке 6 можно проверить, как момент инерции площади сечения варьируется сообразно с координатной осью.

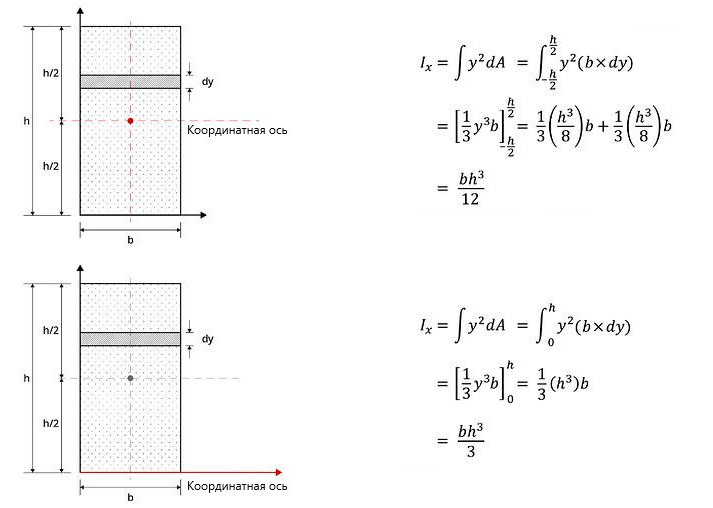
Рисунок 6. Пример изменения момента инерции в зависимости от местоположения координатной оси

Можно наблюдать, насколько отличается момент инерции прямоугольного сечения, когда координатная ось расположена в центре тяжести поперечного сечения и когда координатная ось расположена по оси x.

Калькуляторы свойств коробчатого сечения и двутаврового сечения в Excel

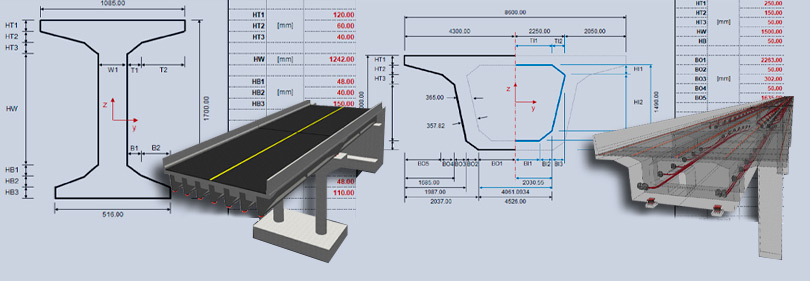
В разделе «Поддержка – Пособия – Калькуляторы» вы можете скачать шаблоны калькуляторов свойств двутаврового и коробчатого сечения в формате Excel. Просто вводите требуемые размеры сечений и получайте результаты для центра тяжести поперечного сечения, момента инерции площади поперечного сечения и момента инерции двутавровых сечений.