Ванты могут выдерживать стационарную и динамическую нагрузку мостов, пролет которых достигает 1000 м. Это качество вантовых мостов делает их более привлекательными и одновременно сложными для инженеров. Вантовые мосты состоят из вант, балки жесткости и пилонов. В данной статье мы рассмотрим автоматизированные способы для получения необходимых сил натяжения вант.
Итак,
Трос состоит из множества прядей, тогда как стержень имеет сплошное поперечное сечение.

Рисунок 1. Поперечные сечения кабеля и стержня
В основном мы создаем предварительное натяжение вант для того, чтобы уменьшить изгибающий момент в пролетном строении. Меньший момент означает более легкие балки, что снижает собственный вес конструкции. Кажется интересной концепцией, не так ли? Но расчет усилий натяжения вант может быть немного запутанным. Натяжение каждой отдельной ванты влияет на усилия в соседних вантах, а также на усилия в балке и пилонах. Не нужно волноваться! Сегодня мы обсудим два инструмента: «Коэффициент неизвестной нагрузки» и «Регулирование усилий в вантах» — все будет достаточно просто и понятно.
Коэффициент неизвестной нагрузки
Функция «Коэффициент неизвестной нагрузки» в midas Civil вычисляет начальное предварительное натяжение (начальное усилие троса), которое необходимо приложить к тросам. Для этого необходимо наложить на элементы модели определенные ограничения, согласно которым внутри конструкции будут генерироваться целевые функции и будет предоставлено оптимальное решение.
Ограничения могут быть в виде величины изгибающего момента в балке или прогиба вершины пилона или сил натяжения вант. Ограничение может быть любым. Для верхнего узла пилона рекомендуется предусмотреть незначительное смещение. Если этого не сделать, то для удовлетворения других ограничений программное обеспечение может предоставить решение, предусматривающее сильное отклонение пилона. В итоге программа автоматически вычислит величины сил предварительного натяжения для каждой ванты, которые будут удовлетворять заданным ограничениям.
Регулирование усилий в вантах
Поскольку поиск коэффициентов неизвестной нагрузки является итеративным процессом, как правило, мы не можем получить усилия натяжения вант, удовлетворяющие всем требованиям инженера, за один раз. Мы можем точно настроить усилия предварительного натяжения, используя матрицу влияния, чтобы получить такое усилие в вантах, которое создает желаемые изгибающие моменты и деформации. Инструмент «Регулирование усилий в вантах» позволяет пользователю регулировать усилие троса и контролировать усилия и смещения в балке или пилонах в режиме реального времени, без повторного анализа конструкции.
Давайте рассмотрим небольшой пример, чтобы понять эту концепцию.
Пример подбора усилий натяжения в вантах
Расчетная модель представляет собой классическую схему симметричного трехпролетного вантового моста с
Усилия в вантах единичные, величиной 1кН. Для каждой ванты создано отдельное загружение, для которых и будут подбираться величины натяжений. Так как расчетная модель симметричная, в каждое загружение входит две ванты, которые будут иметь одинаковое усилие натяжения. Расчетная модель с обозначением нагрузок предварительного натяжения в вантах и нумерацией элементов балки жесткости представлены на рисунке 2.
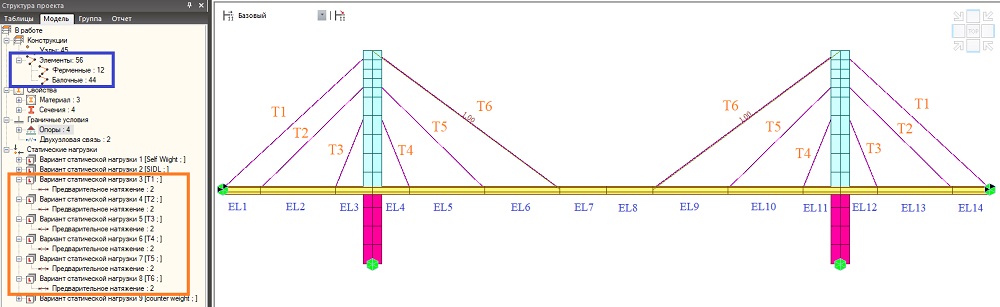
Рисунок 2. Расчетная модель
Также было создано одно сочетание с именем «ULC», объединяющее все постоянные нагрузки и нагрузки единичных натяжений вант. Данное сочетание будет использоваться для подбора усилий натяжения.
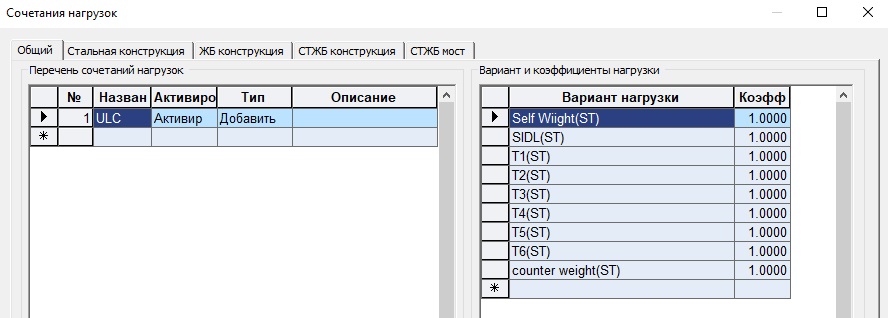
Рисунок 3. Сочетание нагрузок
Инструмент подбора усилий натяжения станет доступным только после выполнения расчета. Выполним его и, прежде чем перейти к подбору усилий, оценим изгибающие моменты в балке и пилонах, а также деформации от сочетания «ULC».
Максимальный изгибающий момент в балке жесткости составляет My_max = 115600кН*м, минимальный My_min = -187800кН*м
Минимальный изгибающий момент в пилоне составляет My_min = -306270кН*м.
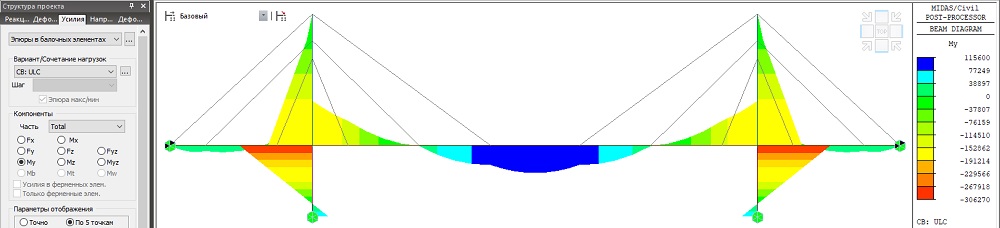
Рисунок 4. Эпюра изгибающих моментов My в балке и пилонах (кН*м)
Вертикальные перемещения балки жесткости в середине центрального пролета Dz = -0.754 м. Горизонтальные перемещения верха пилона Dx = 0.201 м в сторону центрального пролета.
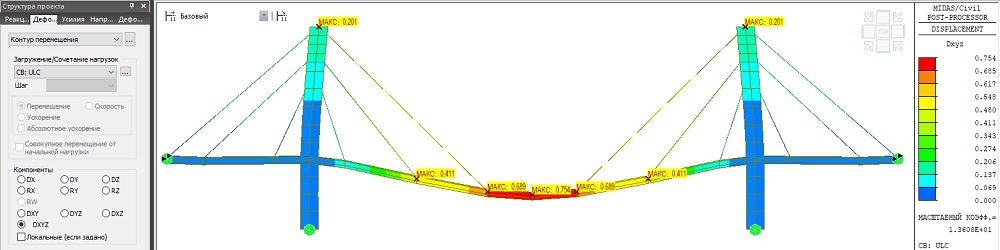
Рисунок 5. Деформации элементов расчетной модели (м)
Теперь я хочу знать, каким должно быть предварительное натяжение тросов в готовом состоянии моста. Воспользуемся методом «Коэффициент неизвестной нагрузки», который находится в «Результаты» — «Мост» — «Регулирование вант». Зададим название случая регулирования «Reg», а также выберем созданное нами ранее сочетание «ULC», по которому и будет осуществляться подбор усилий в вантах. Программе можно указать ограничения для подбора усилий. Такими ограничениями могут быть значения опорных реакций, перемещения узлов или усилия в балочных или ферменных элементах. В этом примере я задам ограничения по величине изгибающего момента в элементах балки жесткости (элементы с 1 по 6). Ограничим величины изгибающего момента My = ± 20000кН*м. В нашем случае неизвестными являются нагрузки T1 — T6, отметим их галочками. Постоянные нагрузки всегда будут учитываться с коэффициентом нагрузки равными единице.
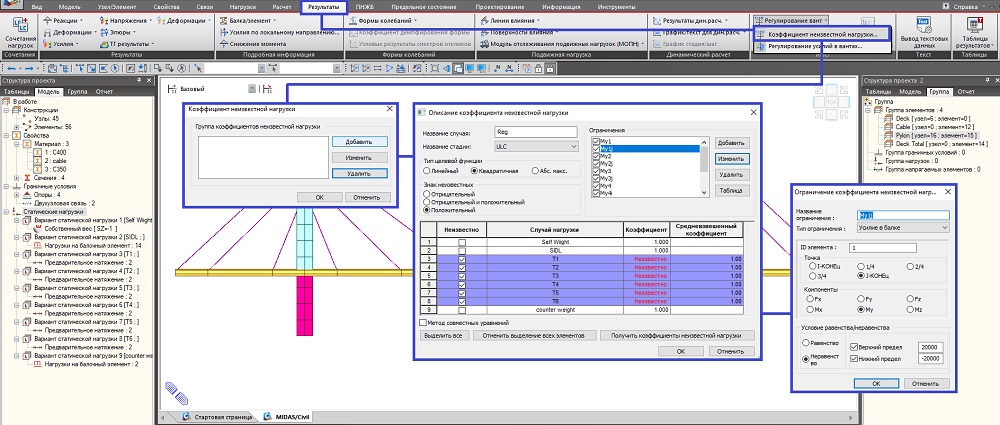
Рисунок 6. Добавление ограничений в элементы балки жесткости для подбора усилий в вантах
Добавлять ограничения можно также в табличном виде. Нажмем на «Таблица» и перейдем во вкладку «Усилия в балке». Параметры данной таблицы можно легко скопировать или добавить новые данные, используя Ctrl+C и Ctrl+V.
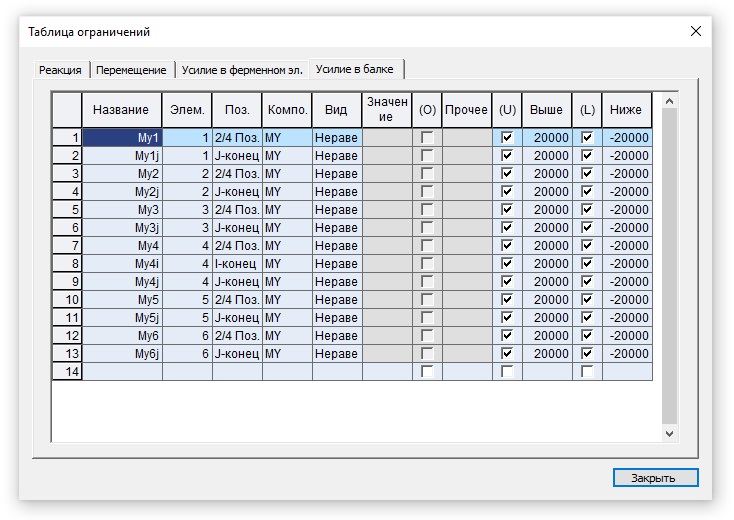
Рисунок 7. Табличный вид наложенных ограничений на элементы балки жесткости
После окончания ввода всех исходных данных для подбора нажмем на «Получить коэффициенты неизвестной нагрузки». После вычислений программа отобразит таблицу с найденными коэффициентами. На рисунке 8 приведены коэффициенты к усилиям T1 — T6, а также значения изгибающих моментов My в элементах балки от данных усилий совместно с постоянными нагрузками. Можно увидеть, что усилия в балке не превышают 20000кН*м.
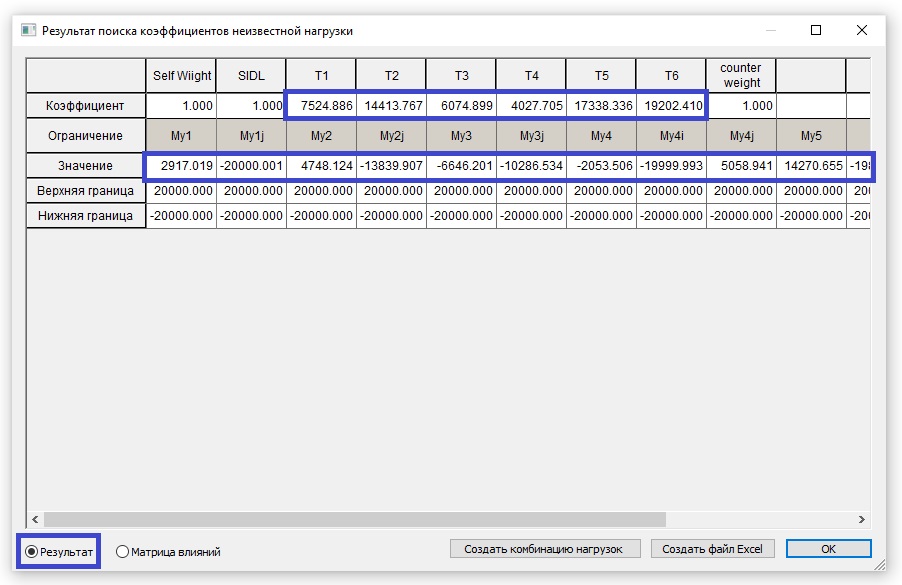
Рисунок 8. Отображение результата по подбору усилий натяжения вант
Отобразим матрицу влияния и нажмем на клавишу «Создать файл Excel», таким образом, отображаемая таблица будет перенесена в Excel. По данной матрице можно понять, как сильно каждая из нагрузок влияет на усилия в главных балках (в которых были введены ограничения). Например, мы можем видеть, что в середине первого элемента изгибающий момент My = 2917кН*м. Данное значение было получено перемножением коэффициентов к нагрузкам (
В начале четвертого элемента изгибающий момент равен предельному ограничивающему значению My = -20000кН*м. По данной матрице видно, что в этом элементе значение момента от постоянны нагрузок составляет My = -157213 -31429.8 +830.7 = -187812.5кН*м. Натяжение каждой ванты уменьшает изгибающий момент, при этом максимальный вклад вносит пятая ванта, уменьшая этот момент на 70035кН*м. Матрица влияния и вычисления усилий приведена на рисунке 9.
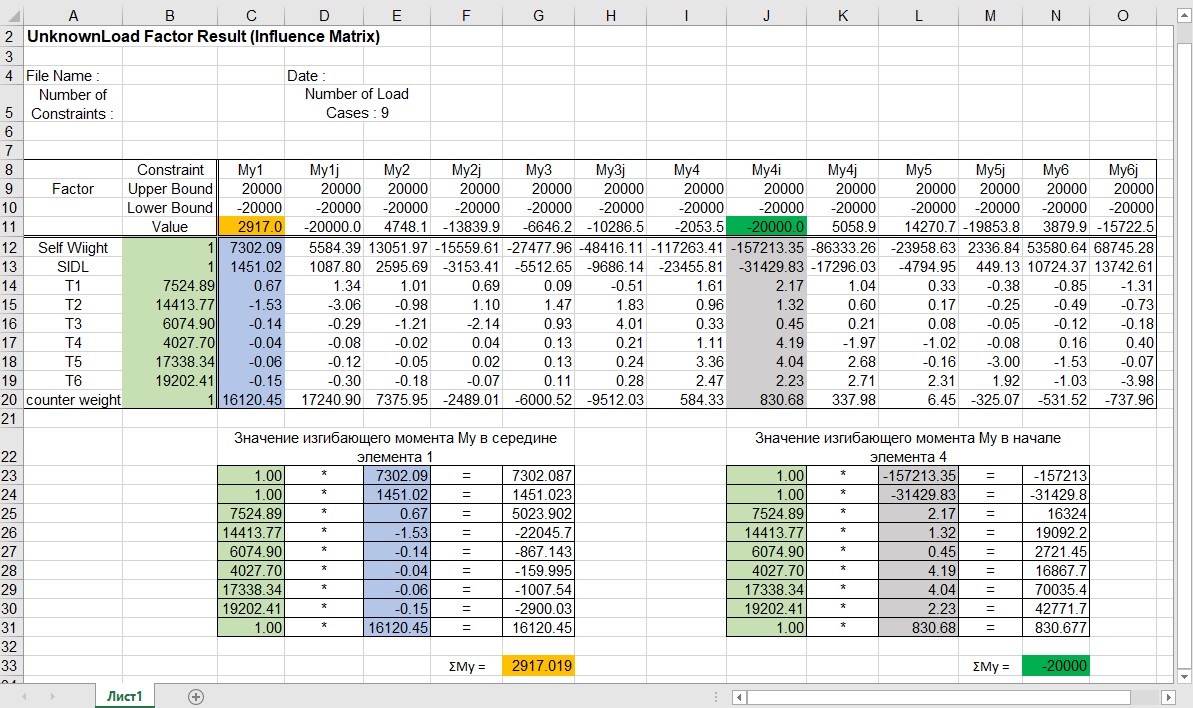
Рисунок 9. Матрица влияния каждой из нагрузок на усилия в главных балках
Нажмем на клавишу «Создать комбинацию нагрузок», укажем имя нового сочетания «Comb» и создадим его. На рисунке 10 показано данное сочетание.
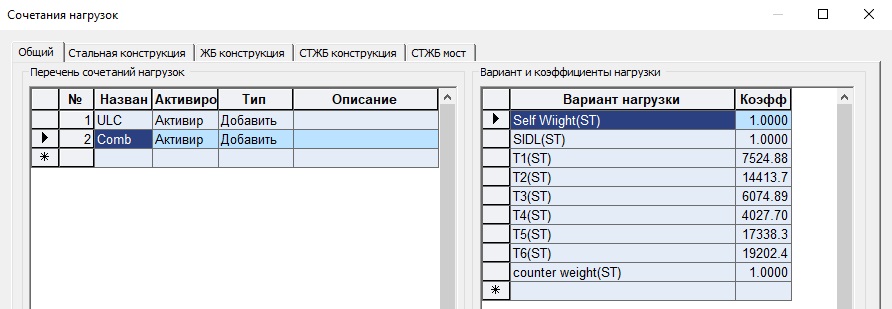
Рисунок 10. Сочетание с вычисленными усилиями в вантах
Из результатов видно, что изгибающий момент в пилонах и в балке жесткости значительно уменьшается, когда мы применили полученное предварительное натяжение в вантах. Момент в пилонах уменьшился почти в 3 раза и составляет My = -107279кН*м. Изгибающие моменты в балке не превышают ±20000кН*м.
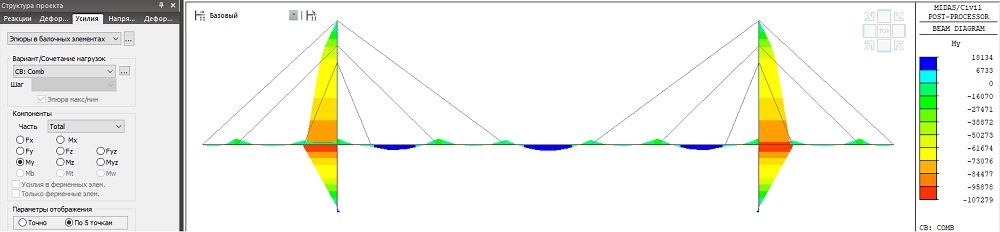
Рисунок 11. Эпюра изгибающих моментов My в пилонах после натяжения вант (кН*м)
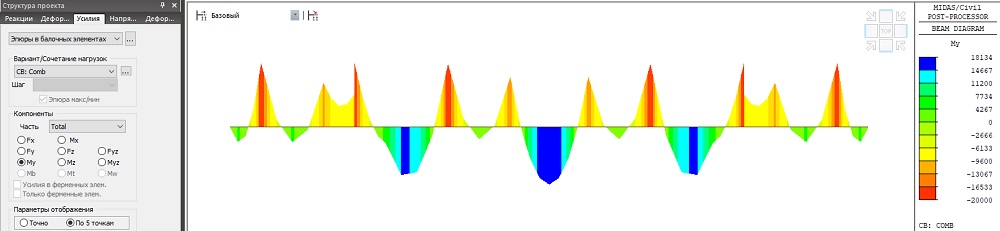
Рисунок 12. Эпюра изгибающих моментов My в балке жесткости после натяжения вант (кН*м)
Также почти в 2 раза уменьшились горизонтальные перемещения верха пилона, сейчас они составляют Dx = 0.111 м. Вертикальные перемещения балки жесткости не превышают Dz = 0.043 м.
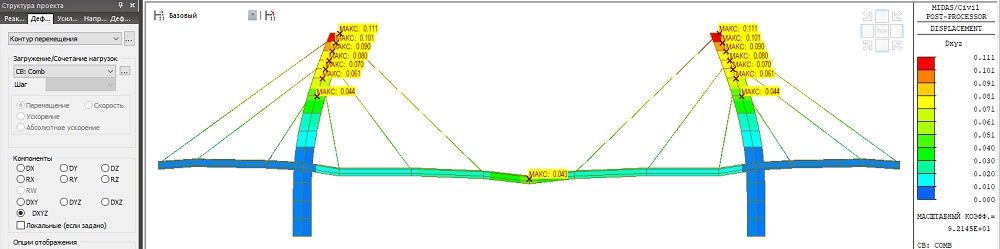
Рисунок 13. Деформации элементов расчетной модели после натяжения вант (м)
Теперь можно перейти к более тонкой настройке усилий натяжения вант. Для этого воспользуемся инструментом «Регулирование усилий в вантах», который находится в «Результаты» — «Мост» — «Регулирование вант». Процесс подбора усилий натяжения вант инструментом «Коэффициент неизвестной нагрузки» является итеративным и может потребовать много времени для поиска идеального состояния. Инструмент «Регулирование усилий в вантах» облегчает этот процесс, так как он вычисляет влияние натяжения вант (коэффициентов нагрузки) на перемещения, усилия в элементах и напряжения с помощью матрицы влияния и отображает изменения на графике в реальном времени. На рисунке 14 продемонстрировано, как выглядит интерфейс регулирования усилий в вантах.
В верхнем блоке приведены значения предварительного натяжения вант, полученные методом поиска «Коэффициента неизвестной нагрузки». Данные значения можно изменять.
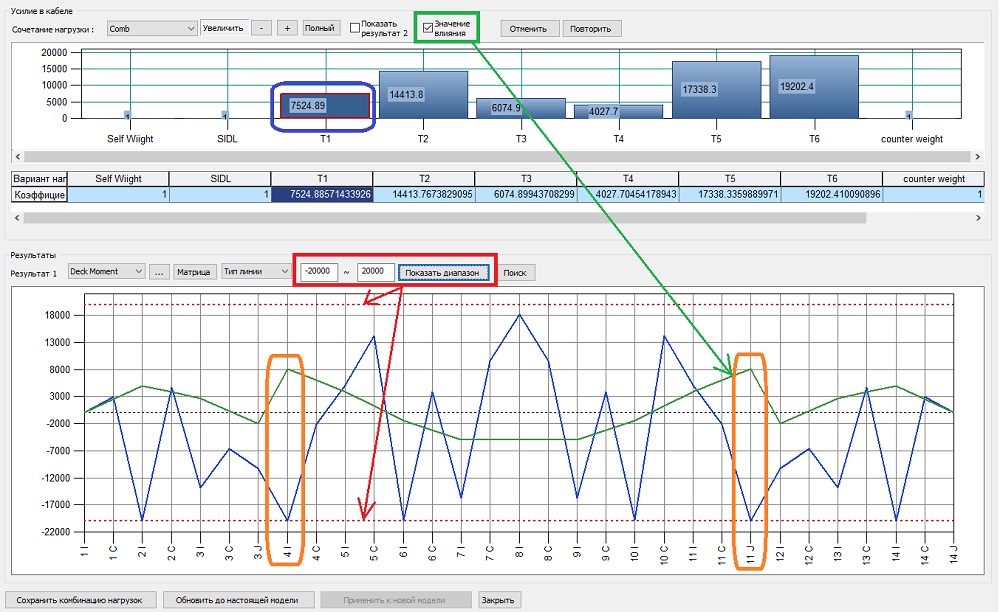
Рисунок 14. Интерфейс инструмента для регулирования усилий в вантах (ванта 1)
В нижнем блоке мы видим синим цветом эпюру изгибающих моментов My в элементах балки жесткости от созданного нами сочетания «Comb», в которое входят усилия натяжения вант. Зеленым цветом показана линия влияния натяжения ванты T1 на изгибающие моменты в балке. Можно заметить, что натяжение первой ванты больше всего влияет на усилия в начале первого элемента и конца одиннадцатого — это место опирания балки на пилоны (выделено оранжевым цветом). Натяжение первой ванты будет увеличивать момент в этих местах сильнее, чем в других. Красным цветом показан диапазон предельных значений изгибающих моментов, который можно установить самостоятельно, как ориентир.
На рисунке 15 показана та же эпюра изгибающих моментов My, но с нанесенной линией влияния ванты T2. Можно заметить, что данная ванта в большей степени влияет на усилия в элементах 2i и 14i (это места прикрепления второй ванты к балке), причем увеличение натяжения будет уменьшать величину изгибающего момента. Также для элементов 3j и 12i натяжение второй ванты будет оказывать сильный, но обратный эффект, натяжение второй ванты будет увеличивать величину изгибающего момента в этих элементах.
Таким образом, можно легко определиться с тем, какие ванты необходимо подтянуть или уменьшить натяжение для получения желаемого эффекта. Используя данный интерфейс можно изменить усилия натяжения в каждой ванте и сразу увидеть, какой эффект окажет данное изменение на усилия в балке жесткости.
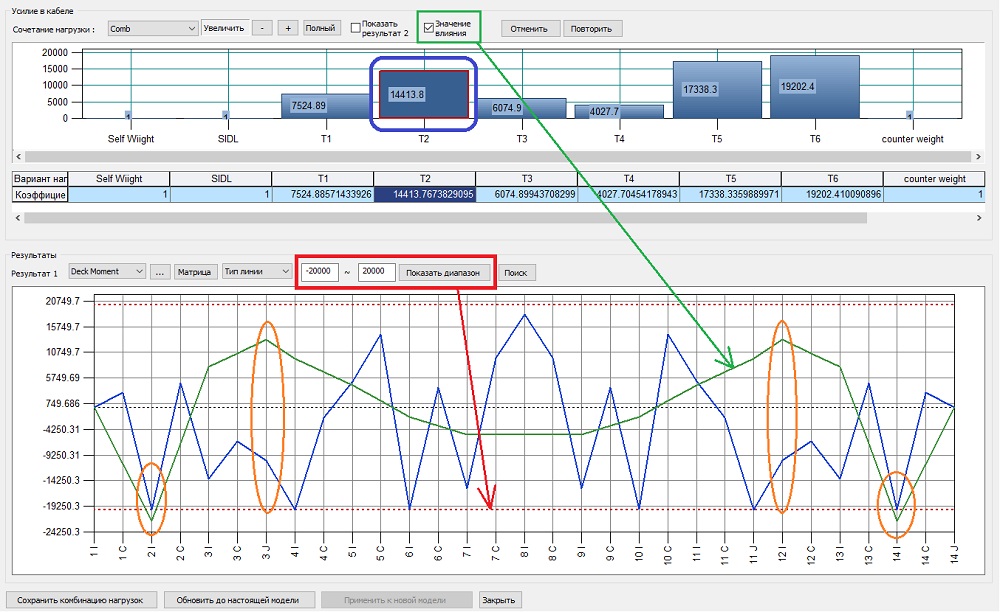
Рисунок 15. Интерфейс инструмента для регулирования усилий в вантах (ванта 2)
Допустим, я хочу скорректировать усилия натяжения в вантах таким образом, чтобы уменьшились горизонтальные перемещения в пилоне с 0.111 м до 0.05 м, что одновременно приведет к уменьшению момента в нем. При этом усилия в балке жесткости не должны возрасти.
Добавим в этот инструмент еще один график, в котором будут отображены перемещения пилона с нанесенной на него линией влияния натяжения вант (здесь можно увидеть, что натяжение первой ванты будет уменьшать горизонтальные перемещения пилона, при том, что на усилия в балке данное натяжение повлияет слабо).
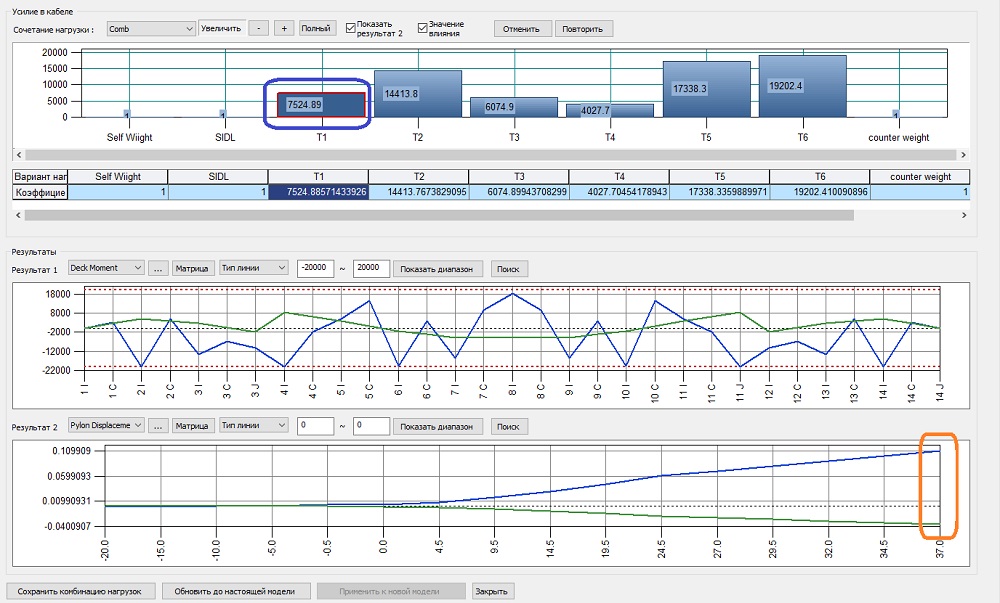
Рисунок 16. Совмещенные графики усилий в балке и перемещений пилона (ванта 1)
Влияние натяжения остальных вант на перемещения верха пилона показаны на рисунке 17. Там же можно увидеть, что максимальный эффект для уменьшения перемещений оказывают первая и вторая ванты. Влияние натяжения остальных вант или минимальное, или вообще носит обратный характер, при котором только уменьшение натяжения будет выпрямлять пилон.
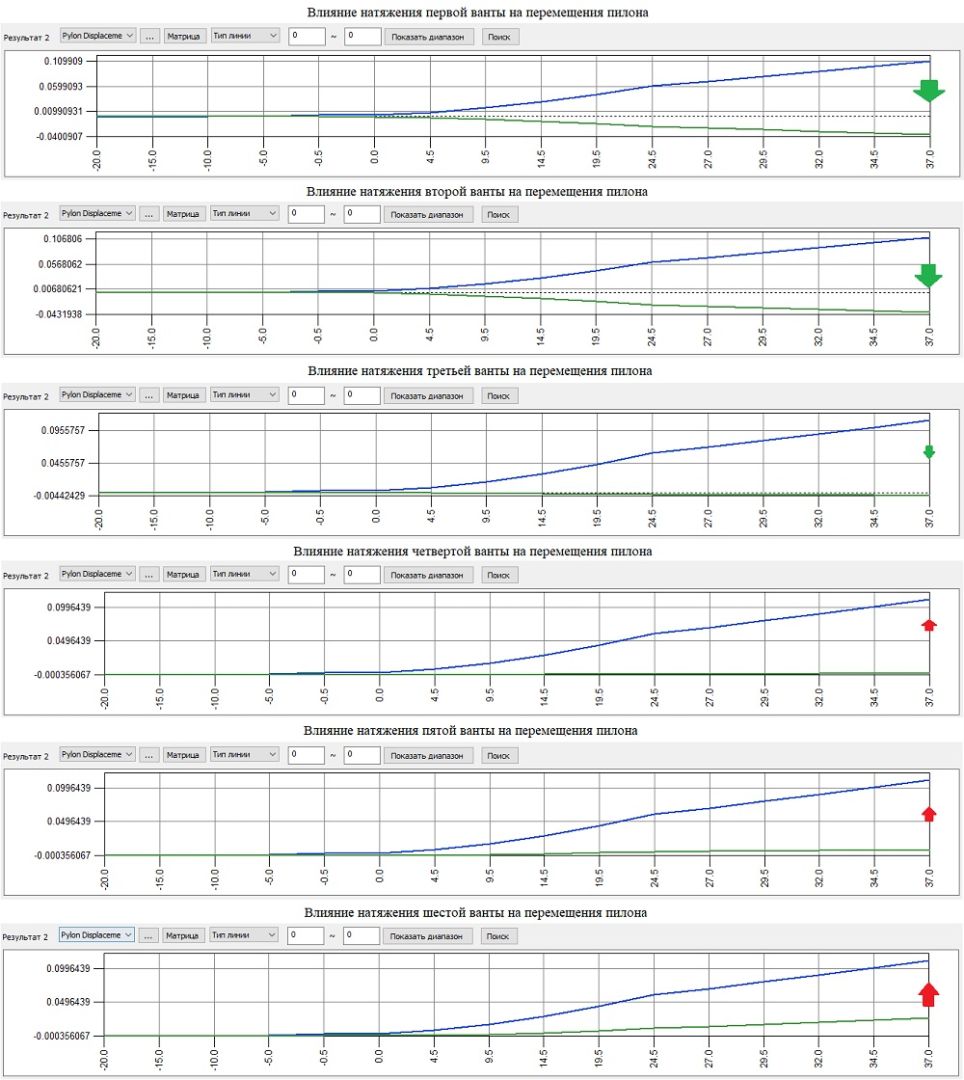
Рисунок 17. Влияние натяжения каждой из вант на перемещения верха пилона
Подтянем первую ванту до значения 12100кН. Перемещения верха пилона уменьшились с 0.111 м до 0.07 м. Уже хорошо, но еще недостаточно. При этом усилия в балке изменились незначительно, лишь в центральном пролете, отрицательные значения стали слегка превышать -20000кН*м.
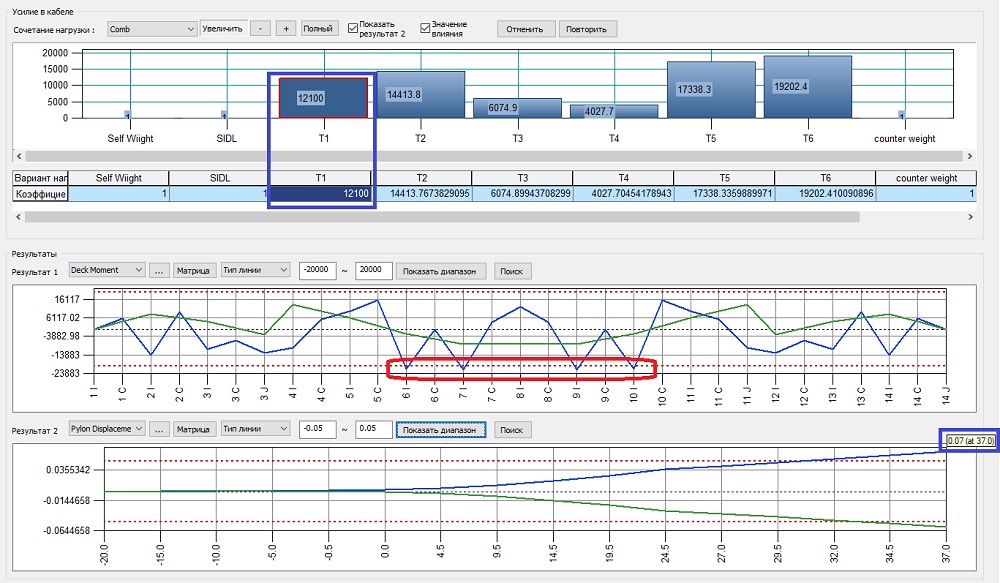
Рисунок 18. Регулирование первой ванты
Подтянем вторую ванту до значения 16500кН. Перемещения верха пилона уменьшились с 0.07 м до 0.06 м. Мы почти у цели.
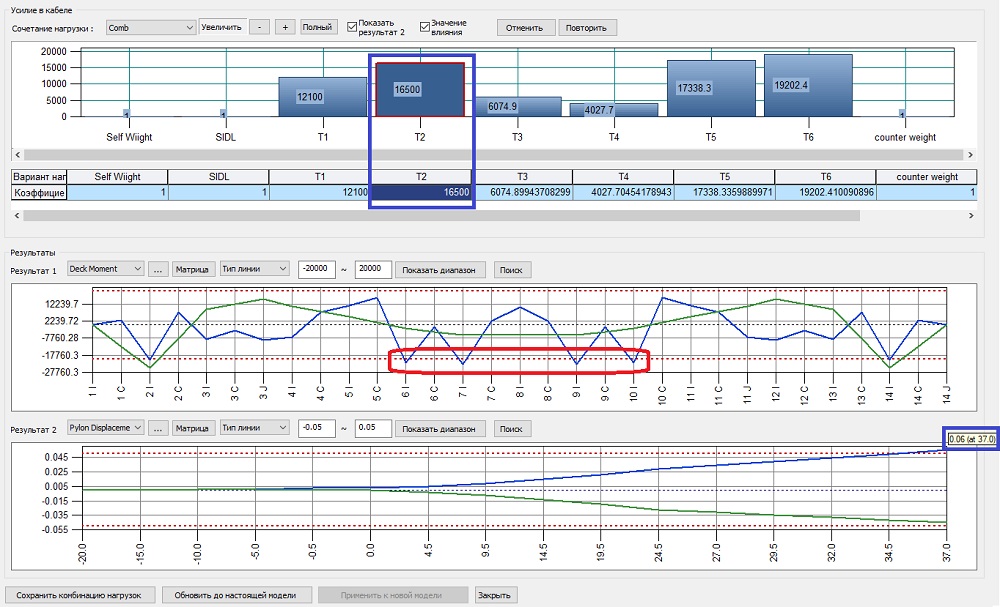
Рисунок 19. Регулирование второй ванты
В итоге, чтобы добиться цели по перемещению верха пилона в 0.05 м, я подтянул третью ванту и слегка ослабил четвертую, пятую и шестую. Результат регулирования усилия показан на рисунке 20. При этом усилия в элементах балки жесткости не превышают заданных нами ограничений ±20000кН*м.
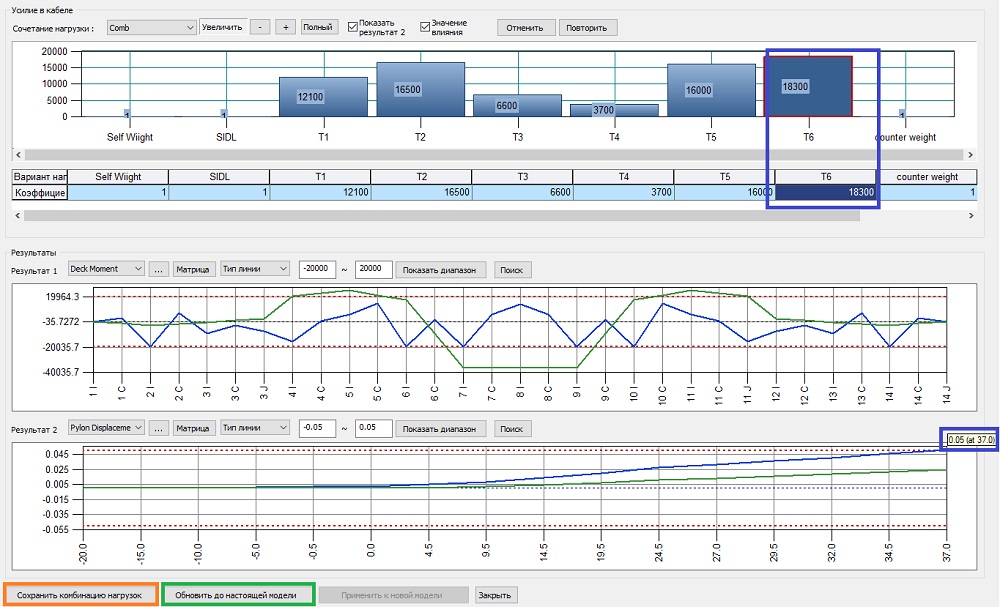
Рисунок 20. Итоговый результат регулирования усилий в вантах
Клавишей «Сохранить комбинацию нагрузок» можно обновить сочетание «Comb», сохранив в нем новые усилия натяжения вант, полученные в процессе регулирования.
Клавишей «Обновить до настоящей модели» можно заменить единичные силы натяжения вант в загружениях T1 — T6 на значения, полученные в процессе регулирования.
Так выглядят результаты изгибающих моментов и деформаций элементов моста от усилий натяжения вант после их регулирования. Значение изгибающих моментов в пилоне уменьшилось до My = 41800кН*м, перемещение верха пилона уменьшилось до Dx = 0.05 м. Усилия в элементах балки жесткости находятся в пределах от My = -20000кН*м, до My = 15600кН*м.
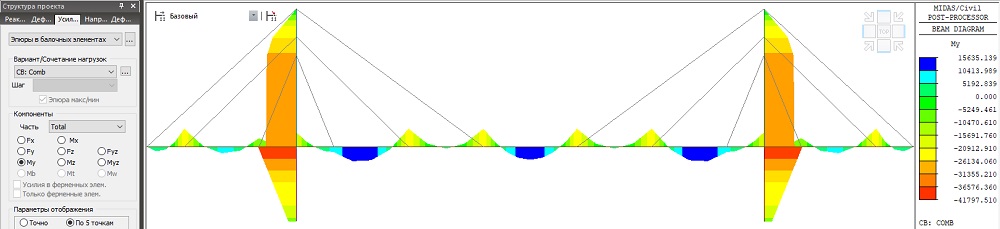
Рисунок 21. Эпюра изгибающих моментов My в пилонах после регулирования (кН*м)
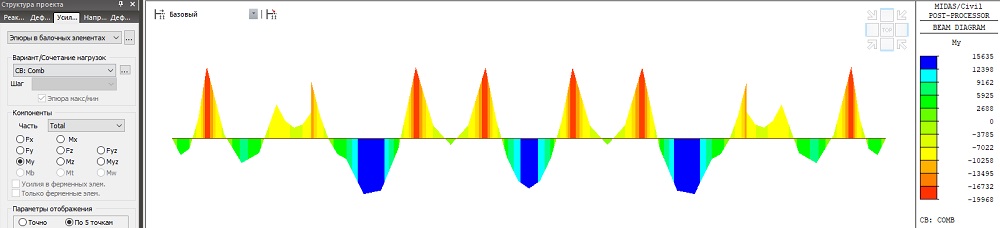
Рисунок 22. Эпюра изгибающих моментов My в балке жесткости после регулирования (кН*м)
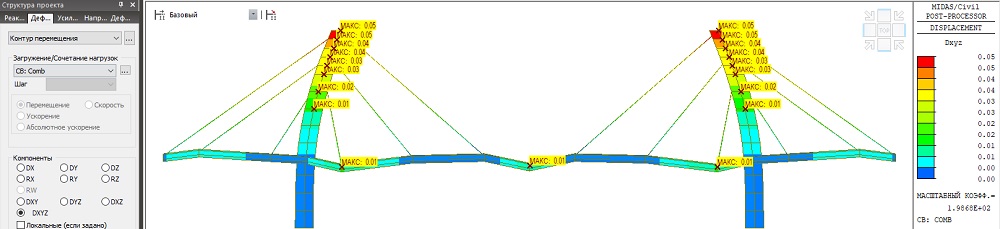
Рисунок 23. Деформации элементов расчетной модели после регулирования (м)
Заключение
При подборе усилий натяжения вант мы сначала воспользуемся модулем «Коэффициент неизвестной нагрузки», который найдет оптимальные коэффициенты нагрузки, удовлетворяющие заданным ограничениям, с помощью оптимизационных методов или решения системы линейных уравнений. Затем мы более точно настроим усилия в вантах в модуле «Регулирование усилий в вантах», используя матрицу влияния, таким образом, быстро и очень просто мы получаем желаемые результаты.

