Во время строительства мост претерпевает изменения в своей конструктивной геометрии, граничных условиях, свойствах материалов с течением времени, а также в порядке и времени действия нагрузки. Эти изменения должны быть рассмотрены, потому что они вызывают различные изменения в напряженно-деформированном состоянии и могут оказывать более критическое воздействие на конструкцию, чем на этапе эксплуатации. В зависимости от типа сооружения и метода строительства вышеописанные изменения могут различаться при возведении предварительно напряженных и просто железобетонных конструкций. Одно остается неизменным: изменение свойств бетона во времени. Данный процесс оказывает влияние на все типы бетонных конструкций.

При расчете предварительно напряженных железобетонных конструкций необходимо учитывать изменения нагрузки, граничных условий и свойств материала (ползучесть, усадка и изменение модуля упругости во времени) бетона на этапе строительства. Кроме того, нельзя забывать о потерях, возникающих в напрягаемой арматуре, в том числе и о потерях, связанных с длительными процессами в конструкции.

В данной статье, которая является частью пособия «Полное руководство по потерям предварительного напряжения», мы разберем реологические процессы, протекающие в бетоне.

Рис. 1. Демонстрация стадий возведения сооружения

Времязависимые свойства материала

С течением времени объем бетонного массива изменяется из-за ползучести и усадки. Подобные изменения создают напряжения в конструкции, которые необходимо учитывать при расчете.

Определение ползучести

Как показано на Рисунке 2, когда на бетон действует нагрузка, в нем возникает первоначальная мгновенная деформация, и даже при отсутствии приложения дополнительной нагрузки со временем в нем возникают дополнительные деформации. Деформации ползучести вначале происходят быстро, но со временем скорость их нарастания снижается. При снятии нагрузки происходит упругое восстановление и восстановление ползучести, но сохраняются остаточные деформации. 

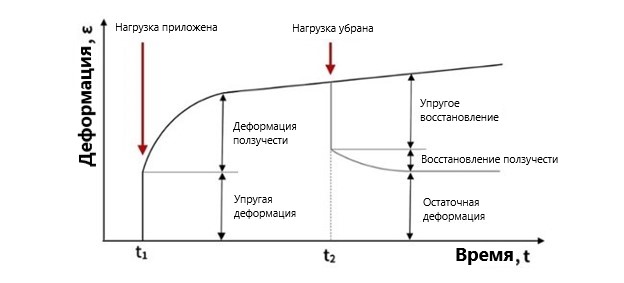Рис. 2. Зависимость деформации от времени при действии ползучести.

На состояние бетонной конструкции оказывают влияние: класс бетона, его возраст и геометрические параметры, водоцементное отношение, условия твердения, продолжительность действия нагрузки и многие другие факторы как внешние, так и внутренние.

Одним из наиболее важных фактов влияния на ползучесть со стороны окружающей среды является относительная влажность воздуха. Если конструкция находится среде с низкой относительной влажностью, в ней возникает дополнительная ползучесть, которая отличается от ползучести, рассматриваемой в данной статье. В общем случае величина относительной влажности учитывается при расчете величины относительной деформации ползучести.

Если величина напряжений от внешнего воздействия находится в пределах упругого диапазона кривой зависимости напряжений от деформаций, то характер изменения напряжений от воздействия ползучести сохраняет то же соотношение. В случае, когда величина длительного напряжения превышает предел пропорциональности, скорость ползучести увеличивается по мере увеличения величины напряжения. Также, очевидно, что чем выше прочность бетона, тем ниже деформации ползучести. Кроме того, восстановление ползучести более вероятно в более старом и сухом бетоне, чем в более молодом и влажном.

Коэффициент ползучести

Коэффициент ползучести и удельная ползучесть, используются для расчета деформаций, вызванных ползучестью. Если приложенное к элементу напряжение постоянно, то, чтобы получить относительную деформацию ползучести, достаточно умножить значение напряжения на величину удельной ползучести. Однако, в большинстве случаев, напряжения конструкции во времени не постоянны. Чтобы оценить данный процесс, предполагается, что в течение короткого промежутка времени величина напряжений остается постоянной. Кроме того, после получения каждой доли деформации ползучести выполняется пересчет напряжений.

В общем виде значение коэффициента ползучести можно вычислить по Формуле 1. В данной формуле C(t,t0) — мера линейной ползучести при постоянных напряжениях; t0 — фактический возраст бетона; Eb(t0) — модуль упругости бетона при фактическом возрасте t0.

Ф. 1. Значение коэффициента ползучести

Вычисление параметров ползучести согласно нормам РФ

Вычисление относительных деформаций ползучести и коэффициентов ползучести в программном комплексе midas Civil выполняется согласно «Методическим рекомендациям по расчету напряженного состояния железобетонных конструкций транспортных сооружений с учетом ползучести и усадки бетона». По данным рекомендациям вычисляется мера линейной ползучести бетона в зависимости от его типа и состава, условий окружающей среды и возраста. На Рисунке 3 представлена последовательность вычисления меры линейной ползучести.

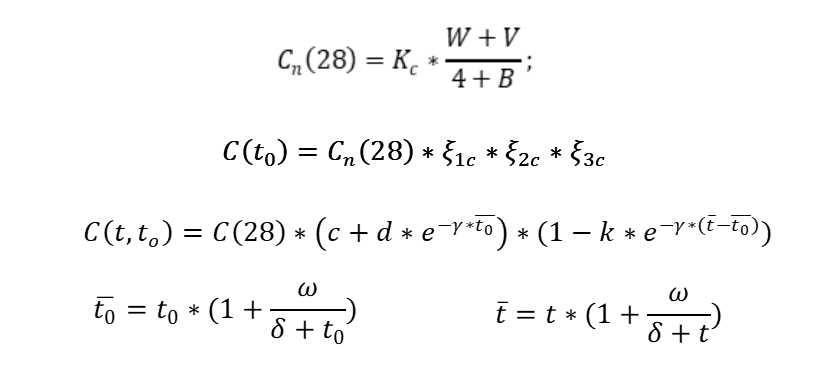
Рис. 3. Формулы для вычисления меры линейной ползучести

В формулах на Рисунке 3:

Cn (28) — нормативное предельное значение меры линейной ползучести бетона, загруженного в возрасте 28 суток;

Kc — безразмерный коэффициент, зависящий от крупности заполнителя бетона;

W — удельное (по объему) количество воды затворения в бетонной смеси, л/м3;

V — удельное (по объему) количество вовлеченного воздуха в уплотненной бетонной смеси, л/м3;

B — класс бетона по прочности на сжатие;

C(t0) — предельное значение меры линейной ползучести;

ξ1c — коэффициент, учитывающий относительную прочность бетона и возраст в момент загружения;

ξ2c — коэффициент, учитывающий величину модуля открытой поверхности элемента;

ξ3c — коэффициент, учитывающий относительную влажность окружающей среды;

C(t,t0) — мера линейной ползучести при постоянных напряжениях, загруженного при разном возрасте, в любой момент времени;

γ, d, k — параметры, учитывающие влияние способа твердения бетона и модуля открытой поверхности;

t0, t — приведенное время;

с = 0,3; ω = 870 сут.; δ = 50 сут.

Подробнее о данных формулах, значениях коэффициентов и порядке расчета Вы можете прочитать в «Методических рекомендациях по расчету напряженного состояния железобетонных конструкций транспортных сооружения с учетом ползучести и усадки бетона».

В качестве тестового примера, рассмотрим задачу. Требуется вычислить меру ползучести и коэффициент ползучести. Исходные данные представлены на Рисунке 4.

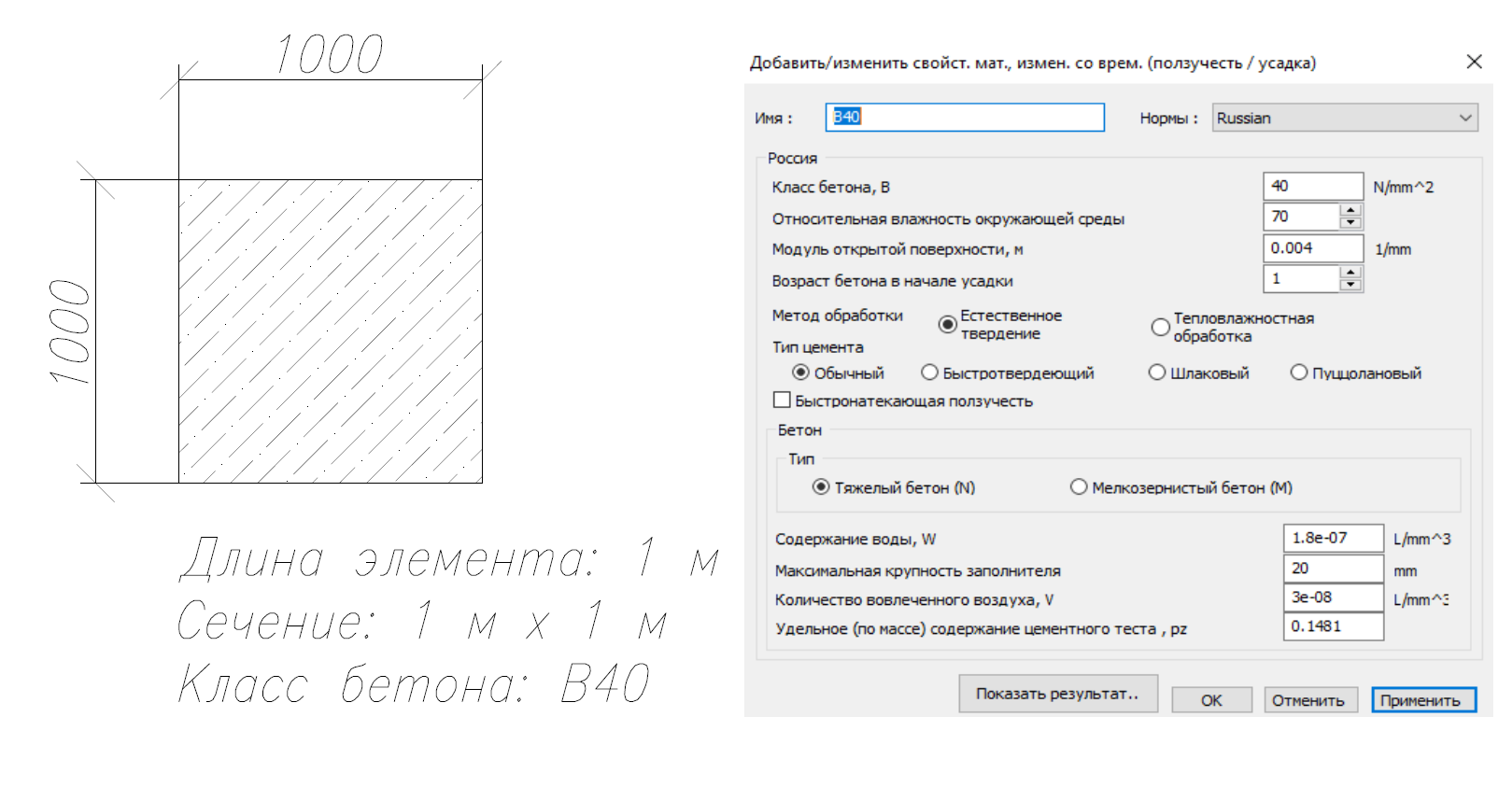
Рис. 4. Исходные данные к Задаче 1

По результатам ручного расчета деформация ползучести на 10028 день при действии сжимающей силы 1000 Н составляет 3,998*10–5 мм, при этом коэффициент ползучести составляет: 3,998*10–5*38493 = 1,5389

Результаты расчета в midas Civil представлены на Рисунках 5 и 6. Погрешность результатов вызвана округлением.

Рис. 5. Результаты деформаций ползучести

Рис. 6. Табличный результат коэффициента ползучести

Определение усадки

В процессе твердения и высыхания бетона вода, не использованная для гидратации, выходит из внутренней части бетона на его поверхность и испаряется. Это явление вызывает усадку бетонного элемента с течением времени, а деформация, вызванная уменьшением объема, называется усадкой при высыхании или усадочной деформацией.

Если рассматривать явление возникновения усадочных деформаций и напряжений более детально, то можно тезисно описать его следующим образом. Вода, находящаяся близко к открытой поверхности бетона, испаряется, в то время как воде внутри бетона требуется время, чтобы добраться до поверхности, вследствие чего высыхание бетонного массива происходит медленно и, что самое главное, неравномерно. Первоначальная усадочная деформация происходит интенсивнее в зоне открытой поверхности, тем самым вызывая растягивающие силы у поверхности бетона, а внутри — сжимающие, для достижения баланса внутренней пары сил. Тем самым в конструкции возникают дополнительные касательные напряжения. В дополнение к этому следует сказать, что усадочные напряжения возникают в конструкции также вследствие того, что элемент может быть стеснен по направлению усадки.

Известно, что факторы, влияющие на ползучесть бетона, влияют и на его усадку. Однако наиболее влияющим фактором является удельное содержание воды в бетоне и относительная влажность окружающей среды. Кроме того, усадочные деформации армированной конструкции меньше, чем у не армированных. Также испарение влаги более интенсивно у элементов с большой площадью открытой поверхности, то есть поверхности, контактирующей с атмосферой.

Вычисление параметров усадки согласно нормам РФ

Вычисление относительных деформаций усадки в программном комплексе midas Civil выполняется согласно «Методическим рекомендациям по расчету напряженного состояния железобетонных конструкций транспортных сооружений с учетом ползучести и усадки бетона». По данным рекомендациям вычисляется предельная относительная деформация усадки бетона в зависимости от его типа и состава, условий окружающей среды и возраста. На Рисунке 7 представлена последовательность вычисления относительной деформации усадки во времени.

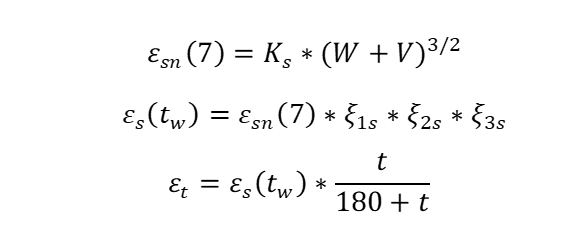
Рис. 7. Формулы для вычисления относительной деформации усадки

В формулах на Рисунке 7:

εsn(7) — относительные деформации усадки по истечении 7 суток;

Ks — безразмерный коэффициент, зависящий от крупности заполнителя бетона;

W — удельное (по объему) количество воды затворения в бетонной смеси, л/м3;

V — удельное (по объему) количество вовлеченного воздуха в уплотненной бетонной смеси, л/м3;

εs(tw) — предельные относительные деформации усадки; ξ1s — коэффициент, учитывающий возраст бетона к окончанию влажного хранения;

ξ2s — коэффициент, учитывающий величину модуля открытой поверхности элемента;

ξ3s — коэффициент, учитывающий относительную влажность окружающей среды;

t — возраст бетона.

Подробнее о данных формулах, значениях коэффициентов и порядке расчета Вы можете прочитать в «Методических рекомендациях по расчету напряженного состояния железобетонных конструкций транспортных сооружения с учетом ползучести и усадки бетона».

В качестве тестового примера, рассмотрим задачу. Требуется вычислить относительную деформацию усадки. Исходные данные представлены на Рисунке 8.

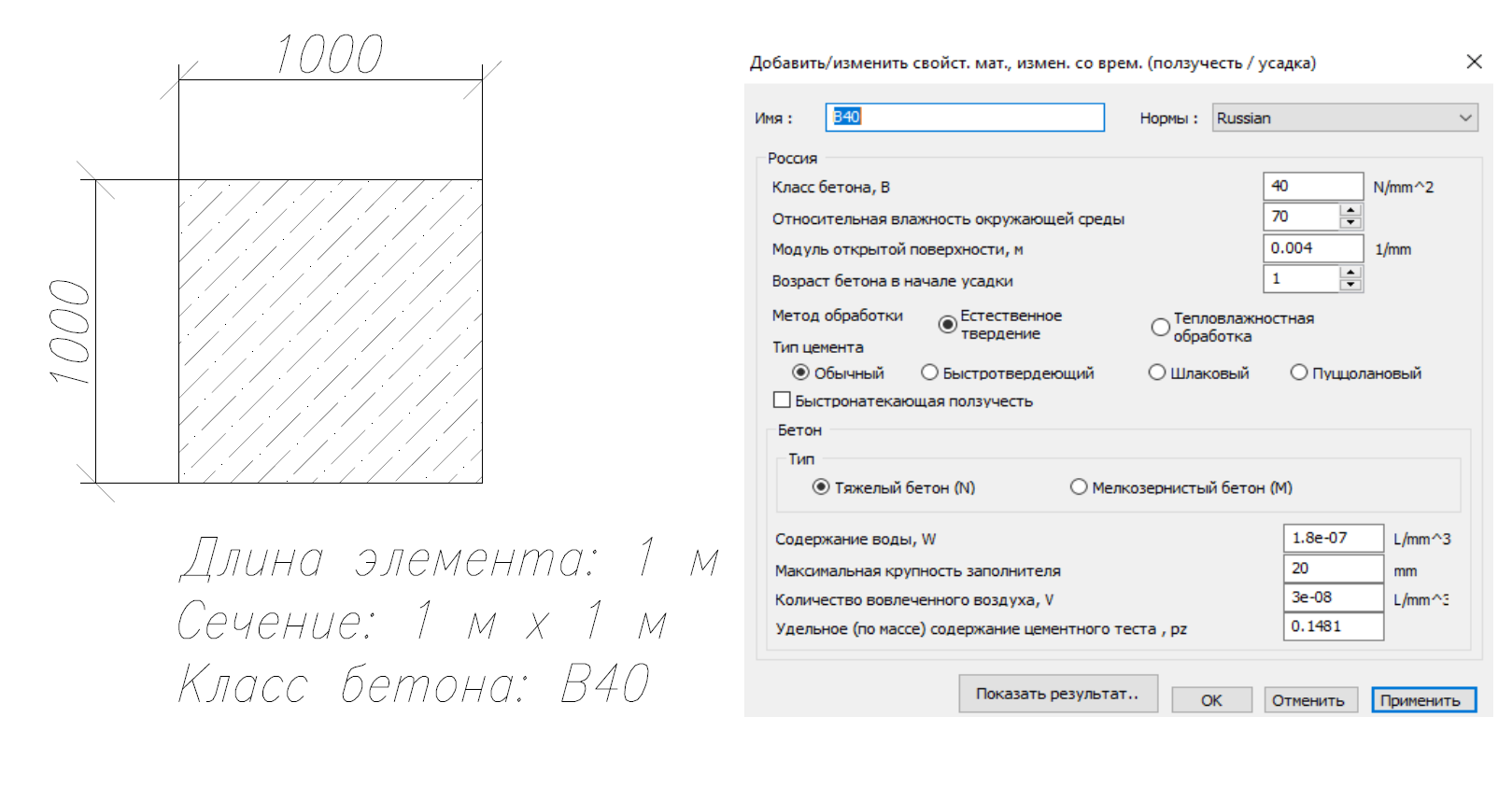
Рис. 8. Исходные данные к Задаче 2

По результатам ручного расчета относительная деформация от усадки бетона составляет 2,03*10–4.

На Рисунках 9 и 10 представлены результаты, полученные в midas Civil.

Рис. 9. Результаты деформаций усадки

Рис. 10. Табличный результат относительных деформаций усадки

Изменение модуля упругости во времени

Поскольку прочность на сжатие и модуль упругости бетона меняются со временем, удельная прочность бетонной конструкции не будет соответствовать проектной до тех пор, пока не пройдет определенное время. В бетонных конструкциях важно разумно учитывать этот эффект старения, чтобы спрогнозировать прочность бетона путем анализа стадий строительства.

Вычисление изменения модуля упругости во времени в программном комплексе midas Civil выполняется согласно «Методическим рекомендациям по расчету напряженного состояния железобетонных конструкций транспортных сооружений с учетом ползучести и усадки бетона».

На Рисунке 11 представлена последовательность вычисления изменения модуля упругости бетона во времени.

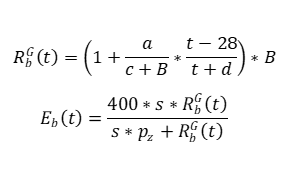
Рис. 11. Формулы для вычисления изменения модуля упругости бетона во времени

В формулах на Рисунке 11:

RbG — гарантированное с обеспеченностью 0,95 значение кубиковой прочности бетона в момент времени t;

a, c, d — коэффициенты, зависящие от вида используемого цемента;

B — класс бетона по прочности на сжатие;

Eb(t) — модуль упругости бетона в момент времени t;

pz — удельное по массе содержание цементного теста;

s — коэффициент, учитывающий влияние вида заполнителя.

Подробнее о данных формулах, значениях коэффициентов и порядке расчета Вы можете прочитать в «Методических рекомендациях по расчету напряженного состояния железобетонных конструкций транспортных сооружений с учетом ползучести и усадки бетона».

Скачайте демо-версию midas Civil

Начните пользоваться уже сегодня! После скачивания демо-версии
вам будут доступны обучающие материалы по началу работы.