В этой статье мы выясним, почему необходимо учитывать геометрическую нелинейность в элементах мостов, и как она влияет на результаты расчетов (усилия и деформации).

Допустим, мы имеем колонну (стойка опоры), и нам нужно найти величину смещения верха колонны и максимальный опорный момент. Типичный случай во время эксплуатации, когда сила P возникает в результате нагрузки от пролетного строения через опорную часть, а сила V возникает в результате действия нагрузки от торможения, центробежной силы или ветровой нагрузки.

Определим опорный момент при P = 4500 тс, V = 50 тс.

Материал колонны — бетон В30, с модулем упругости E = 3314100 тс/м2. Высота колонны L = 45 м, сечение колонны круглое, диаметр d = 3.2 м.

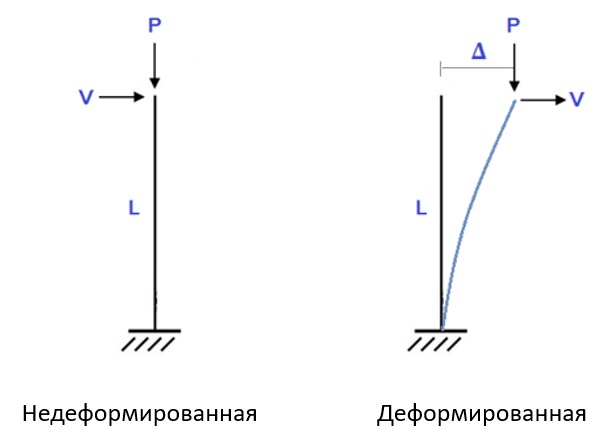
Рисунок 1. Консольная колонна, недеформированная и отклоненная форма

В стандартном линейном статическом анализе опорный момент и верхние деформации можно просто рассчитать как:

На рисунке 2 показаны результаты линейного анализа в midas Civil.

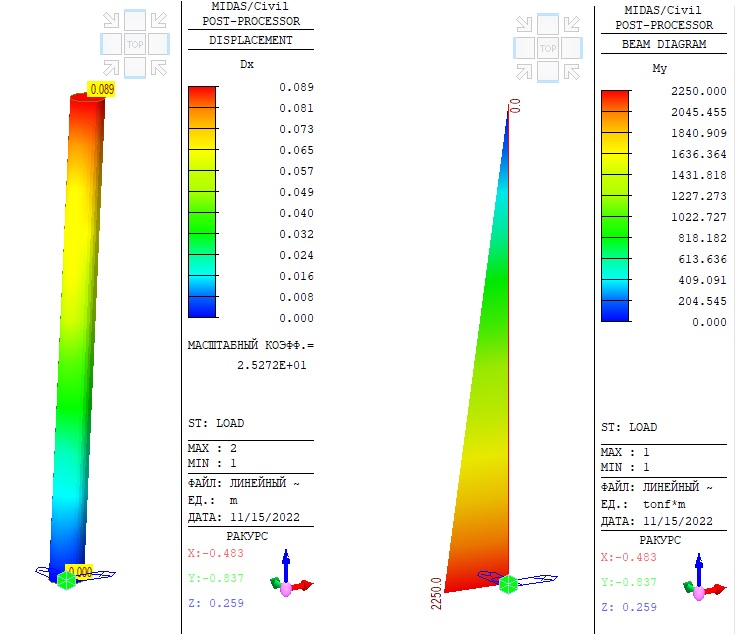
Рисунок 2. Линейный расчет. Деформации колонны и изгибающий момент в корне.

Как мы можем видеть, результаты ручного расчета и линейного расчета в midas Civil очень хорошо совпадают. Тогда зачем беспокоиться о нелинейности? На самом деле, если значения P и (или) Δ велики, они будут способствовать возникновению вторичного момента (M=P * Δ) в корне колонны, который здесь не учитывается. В таком случае нам может потребоваться более сложный анализ.

Геометрически нелинейный анализ

В упрощенном нелинейном анализе:

М = V * L + P * Δ — суммарный изгибающий момент с учетом влияния вторичного момента.

Термин P * Δ представляет собой вторичный момент, вызванный смещением вершины, и поэтому получил название «P-дельта». Это означает, что осевая сила может создать дополнительный опорный момент, когда мы рассматриваем традиционную задачу изгиба колонны. Для расчета деформации верха колонны Δ состоит из Δ1 (верхний горизонтальный прогиб от горизонтальной нагрузки V) и Δ2 (верхний горизонтальный прогиб от вертикальной нагрузки P). Предполагать, что Δ = Δ1 + Δ2 не совсем верно, поскольку правило суперпозиции не выполняется из-за нелинейности. Тем не менее, определим Δ исходя из этих предпосылок, а затем вычислим и изгибающий момент M в корне колонны, как показано ниже:

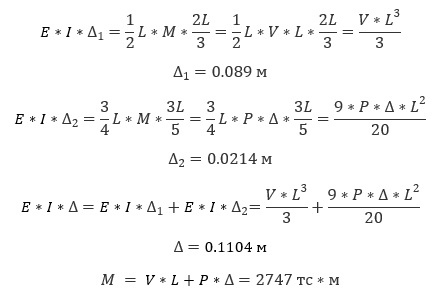
По сравнению с моментом (2250 тс*м), учитывающим только линейный эффект, опорный момент, полученный с учетом вторичного эффекта от смещения вершины, на 22.1% выше. Поэтому нелинейность в этом случае нельзя игнорировать.

Кроме того, линейный расчет предполагает, что кривая отклонения от P и V является кубической (3-й порядок). Это верно только тогда, когда P равно нулю, то есть, когда в элементе нет осевой силы, и когда момент внутри элемента изменяется линейно. При рассмотрении геометрической нелинейности при наличии продольной силы кривые прогиба при осевом сжатии и осевом растяжении не идентичны.

На рисунке 3 показаны результаты геометрически нелинейного анализа в midas Civil с колонной, смоделированной с помощью одного стержневого элемента. На рисунке 4 показан тот же расчет, но с колонной, смоделированной десятью стержневыми элементами. Данный геометрически нелинейный анализ в midas Civil можно задать, если перейти в раздел «Расчет» — «Управление расчетом» — «Нелинейный».

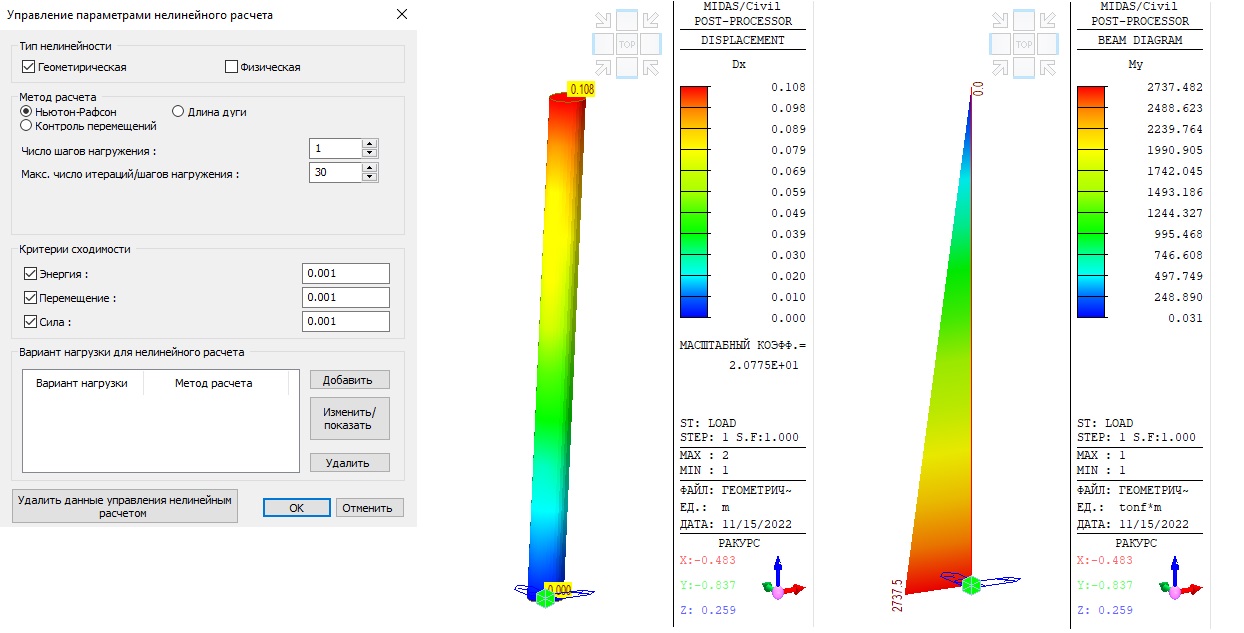
Рисунок 3. Геометрически нелинейный расчет. Колонна, смоделированная одним стержневым элементом. Деформации колонны и изгибающий момент в корне.

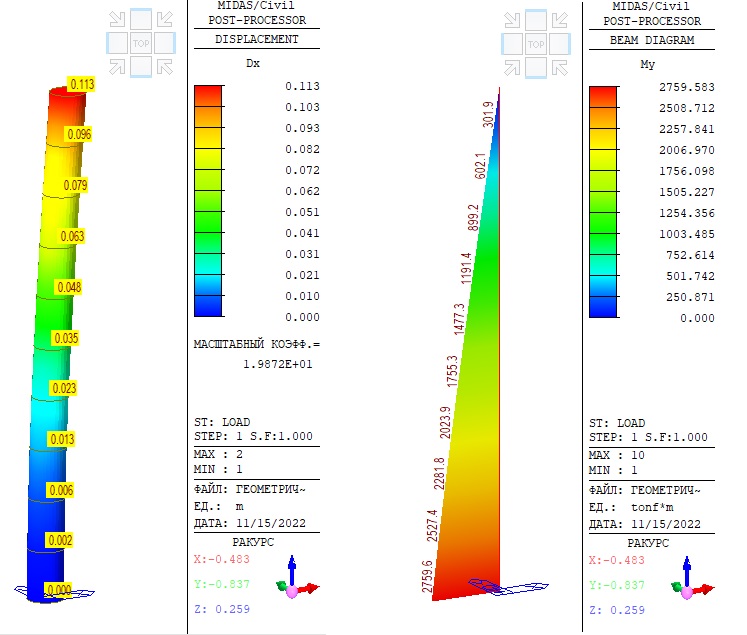
Рисунок 4. Геометрически нелинейный расчет. Колонна, смоделированная десятью стержневыми элементами. Деформации колонны и изгибающий момент в корне.

Почему результаты двух моделей Midas отличаются от ручного расчета? И почему результаты анализа зависят от количества элементов? Как упоминалось выше, кривая прогиба при осевых нагрузках не имеет кубической формы. Однако большинство коммерческих программ, в том числе midas Civil, предполагают кубическую кривую прогиба для балочных элементов. Это дает хорошее приближение только в том случае, если в элементе нет осевой силы или если момент изменяется линейно между узлами. Таким образом, если жесткость постоянна, нет осевой силы и нет нагрузок внутри стержневого элемента, количество делений не будет влиять на результаты расчета. Но, как показано в приведенном выше ручном расчете, наша колонна имеет осевую силу P, а кривая прогиба не является кубической. Следовательно, одна кубическая кривая не может представлять более сложную реальную кривую отклонения, и то, насколько хорошо программное обеспечение аппроксимирует реальное отклонение, зависит от количества делений. Очевидно, что в этом случае задача, состоящая из 10 элементов, дает лучшее приближение, чем из 1.

Анализ P-Delta в midas Civil

P-Delta анализ является частью геометрически нелинейного анализа. Согласно справочнику по расчетам в midas Civil, функция анализа P-Delta дает очень точные результаты, когда боковые смещения относительно малы (в пределах предела упругости). В midas Civil анализ P-Delta составляет уравнения равновесия для исходной формы, но учитывает изменение осевой силы и матрицы жесткости на каждой итерации. Следовательно, правило суперпозиции снова не действует из-за итеративного характера. Более подробно с данным типом расчета можно ознакомиться в документе Анализ Midas Civil, на странице 123.

Чтобы настроить параметры анализа P-Delta в midas Civil, необходимо перейти в «Расчет» — «Управление расчетом» — «P-Дельта». На Рисунке 5 показаны результаты анализа P-Delta для данной колонны.

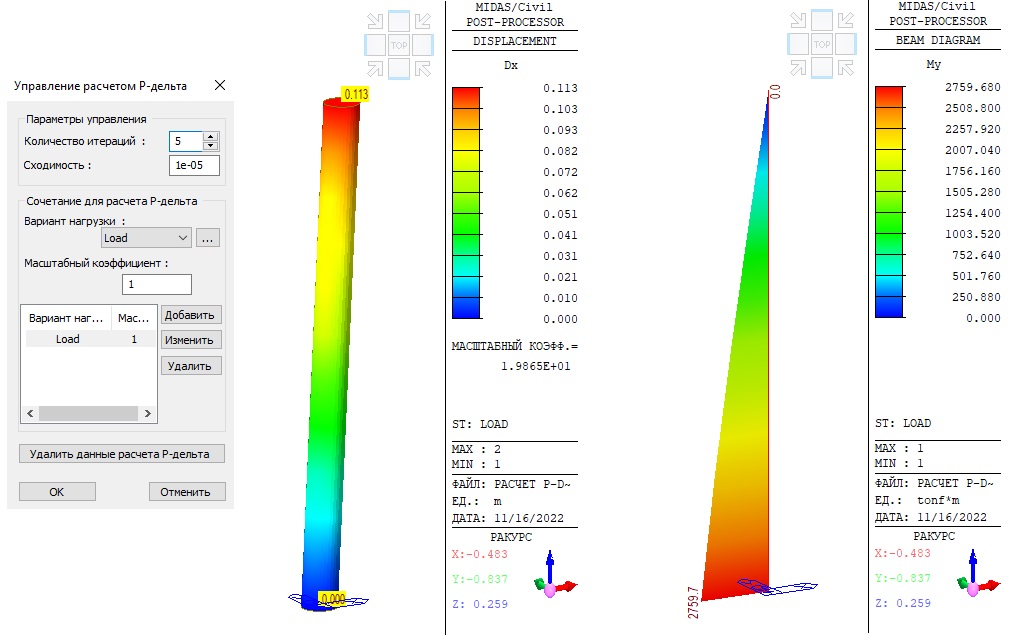
Рисунок 5. Расчет P-Delta. Деформации колонны и изгибающий момент в корне.

Линеаризованный анализ конечных перемещений

Еще один метод, который следует упомянуть, называется линеаризованным анализом конечных перемещений. В этом методе осевая сила в каждом элементе остается постоянной, а это означает, что итерации при расчете не требуются. Другими словами, действует правило суперпозиции, что упрощает инженеру работу. Этот метод можно применять, если изменением осевой силы можно пренебречь, что справедливо для большинства конструкций.

Чтобы задать параметры данного анализа, необходимо перейти в «Нагрузки» — «Начальные силы» — «Малое перемещение» — «Исходные усилия в элементе», далее необходимо добавить начальные силы в элементы. В нашем случае мы добавим начальную сжимающую продольную силу в начале и конце элемента по величине равной внешней действующей сжимающей нагрузки P = 4500 тс. На рисунке 6 показаны результаты линеаризованного анализа конечных перемещений midas Civil.

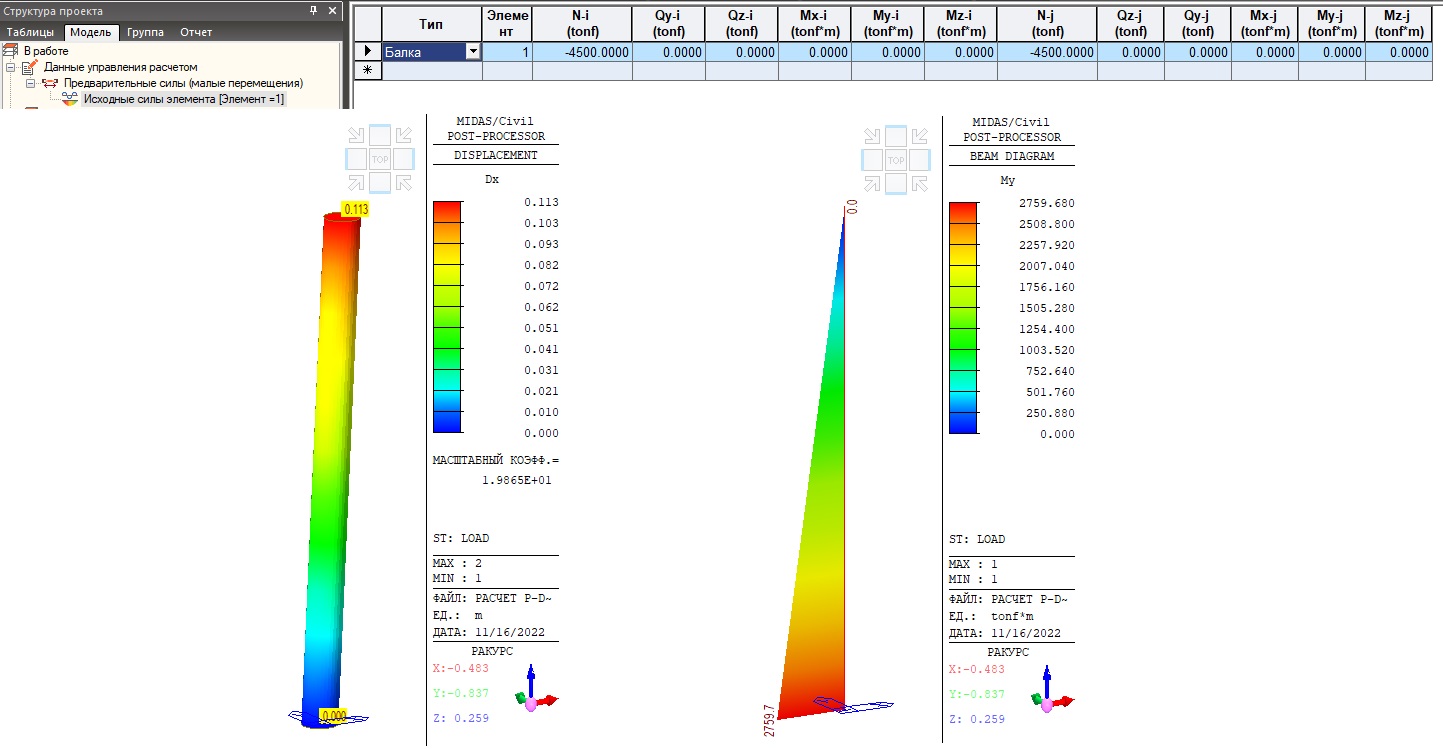
Рисунок 6. Линеаризованный анализ конечных перемещений. Деформации колонны и изгибающий момент в корне.

Мы можем проверить этот результат с помощью ручного расчета. На самом деле, линеаризованный метод конечных перемещений просто учитывает уменьшение жесткости (при осевом сжатии) и увеличение жесткости (при осевом растяжении). Оценить жесткость и получить перемещения верха колонны, можно таким образом:

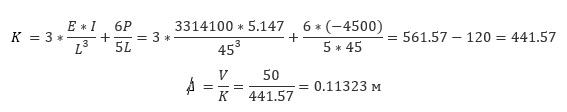
Этот пример очень типичен для мостов средней грузоподъемности. В нашем случае снижение жесткости из-за осевой силы составляет 21%. Поэтому этот эффект необходимо учитывать при проектировании.

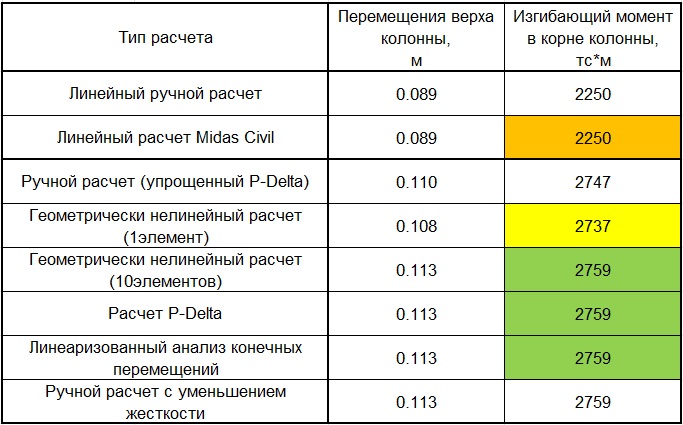
Ниже в таблице 1 приведены результаты с использованием различных расчетов, упомянутых выше. Использование одного балочного элемента в геометрически нелинейном анализе дает результат, который занижает величину нагрузки. Три другие схемы анализа в midas Civil хорошо согласуются между собой.

Таблица 1. Результаты расчета колонны с использованием различных вариантов расчетов

Можно сделать вывод: если сжимающая сила P и (или) горизонтальные перемещения края консоли Δ велики, они будут способствовать возникновению вторичного момента (M=P * Δ) в корне консоли, и нам может потребоваться более сложный вид анализа. В геометрическом нелинейном анализе существует три уровня методов анализа: геометрически нелинейный, P-Delta и линеаризованное конечное перемещение. В первых двух правило суперпозиции не действует, между тем, линеаризованный анализ конечных перемещений во многих случаях дает удовлетворительные результаты.

Пройдите бесплатный вводный курс по midas Civil

Создайте модель СТЖБ пешеходного путепровода и выполните линейный расчет двух типов