В этой статье мы рассмотрим пример, где будет показано, как определяются усилия от усадки бетонной плиты в неразрезных СТЖБ пролетах, а так же попробуем разобраться в том, что несут в себе первичные и вторичные эффекты усилий в программе midas Civil.
Первая задача с расчетом усилий и деформаций от усадки бетона
Рассмотрим пример. Мы имеем двутавровую СТЖБ балку, располагающуюся тремя пролетами длиной 42 м + 63 м + 42 м = 147 м. Материал стали — 10ХСНД. Материал бетона — В35. Задачу будем решать в плоской постановке, в плоскости
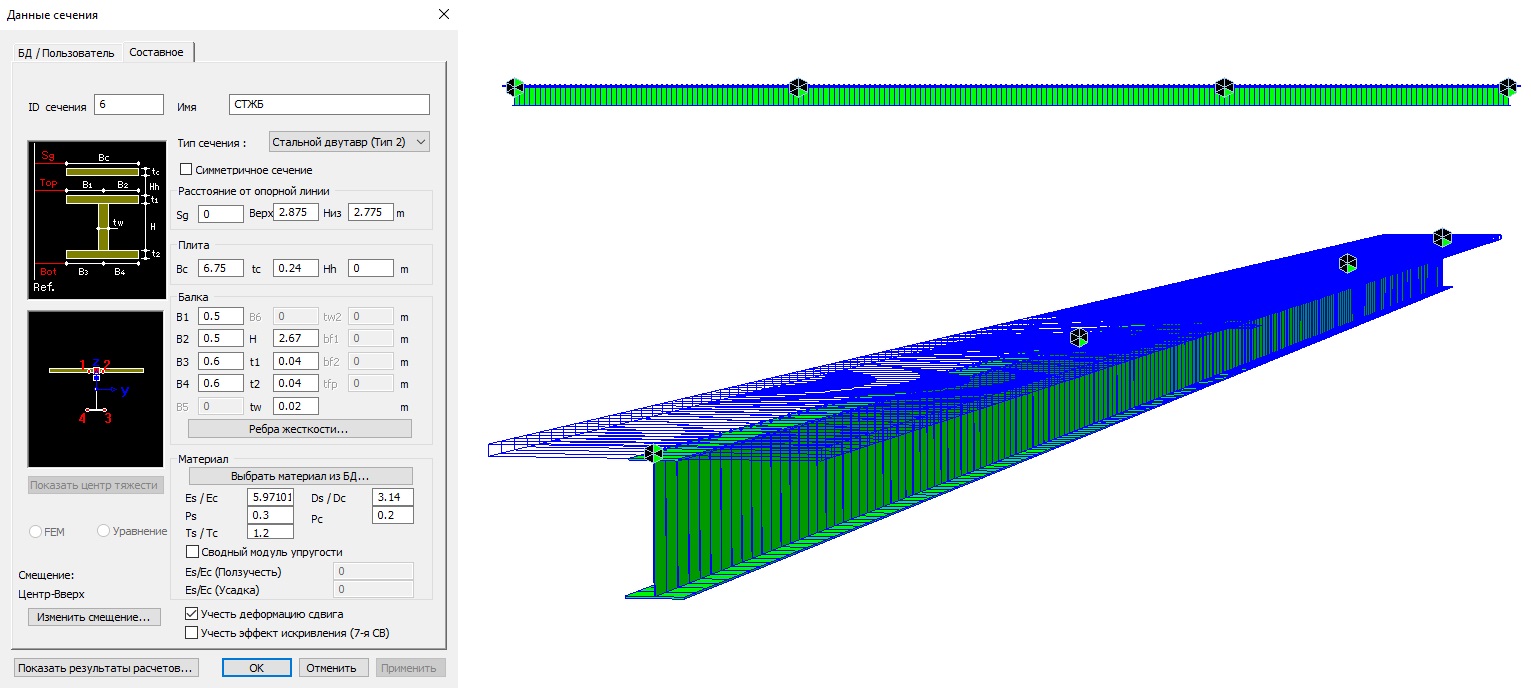
Рисунок 1. Расчетная модель пролетного строения и сечение главной балки
Зададим график усадки. В нашем случае будем использовать пользовательскую кривую, в которой предельное значение относительных деформаций усадки по истечению 100 лет равно 0.0002. Создадим стадийный расчет, в котором на первой стадии активируется только стальная часть балки, а на второй стадии активируется бетонная плита. Из
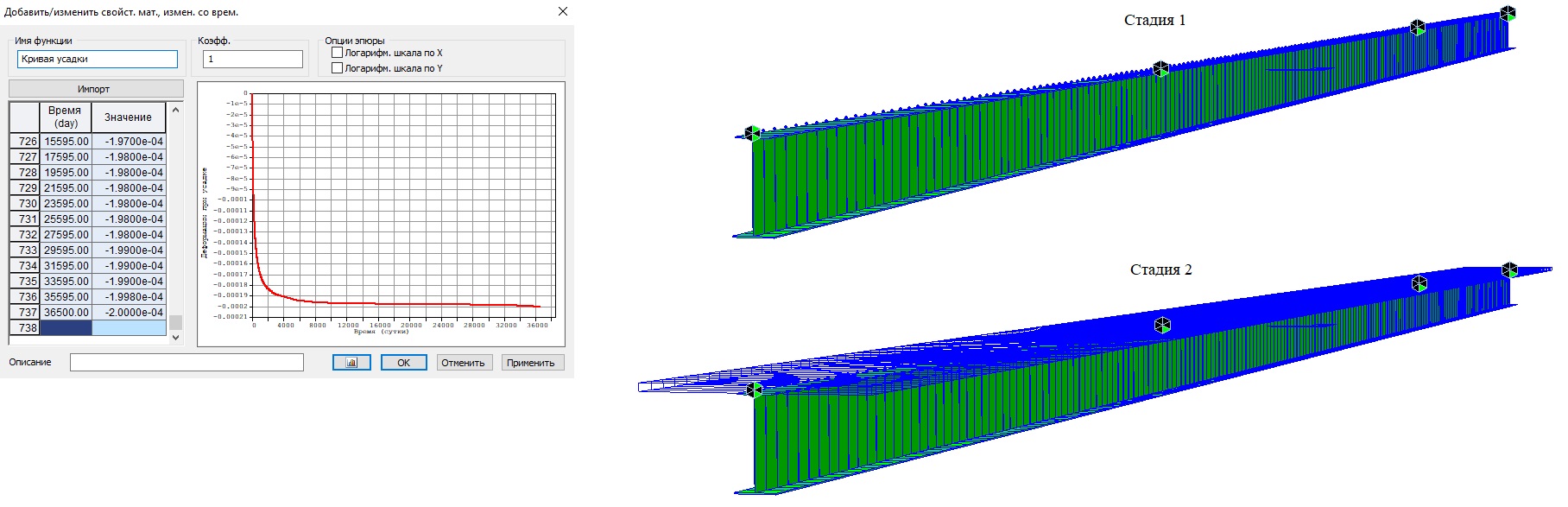
Рисунок 2. График относительных деформаций усадки бетона и стадии работы балки жесткости
Выполним расчет, оценим деформации модели и усилия в её элементах на второй стадии (на первой стадии все значения нулевые,
Деформации модели мы можем отобразить только от первичного эффекта, которые и будут являться искомыми деформациями от усадки бетонной плиты. В нашем случае вертикальные деформации в глобальной оси Z составляют -6.8 мм для боковых пролетов и 4.9 мм для центрального.
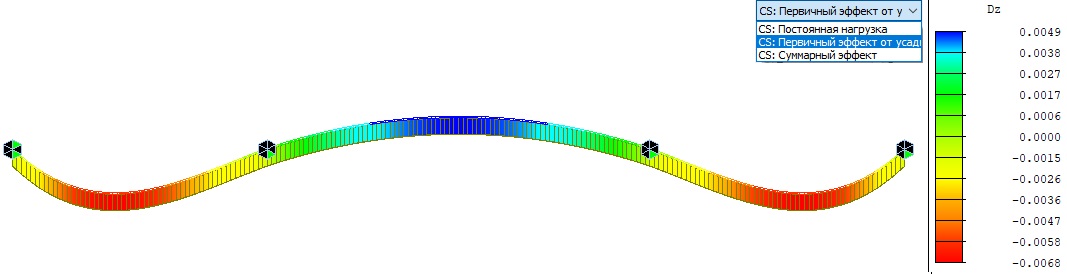
Рисунок 3. Деформации главной балки от усадки бетона по истечении 100 лет
С усилиями ситуация немного запутанней. В результатах мы видим уже и первичный, и вторичный эффекты от усадки.
При этом в первичном эффекте в части 1, которая является стальной балкой, изгибающий момент и продольная сила нулевые, а в части 2, которая является бетонной плитой, мы видим сжатие в 1140тс, при этом изгибающий момент в бетоне также отсутствует.
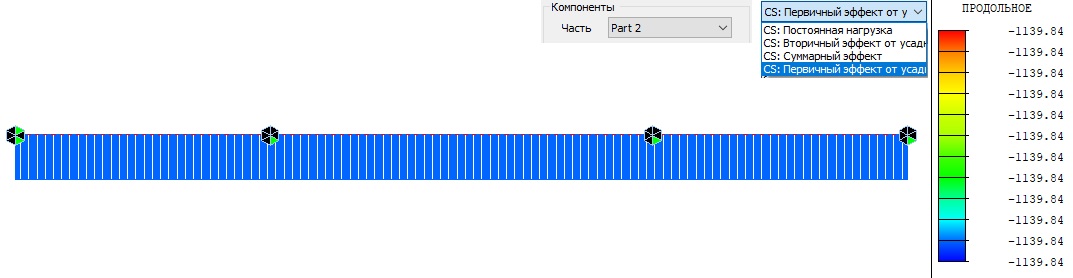
Рисунок 4. Первичный эффект продольной силы в бетонной плите (Часть 2)
От вторичного эффекта усадки, в части 1 (стальная балка), возникает сжимающая продольная сила величиной -178.7тс у крайних опор и -420.6тс в центральном пролете, а также изгибающий момент 279тс*м у крайних опор и -39.6тс*м в центральном пролете.
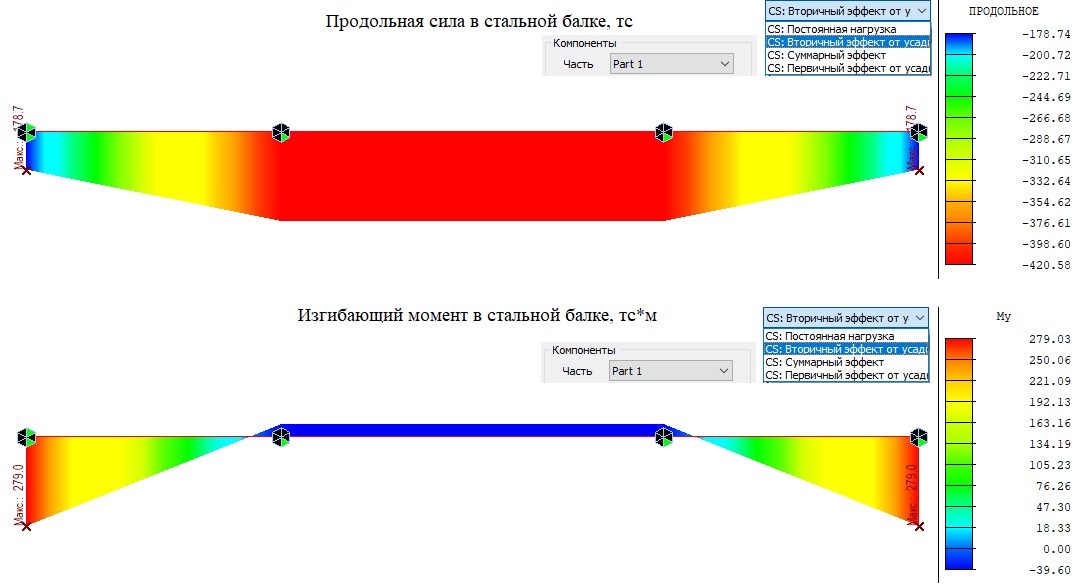
Рисунок 5. Вторичный эффект продольной силы и изгибающего момента в стальной балке (Часть 1)
От вторичного эффекта усадки в части 2 (бетонная плита) возникает такая же продольная сила, но уже растягивающая плиту, величиной 178.7тс у крайних опор и 420.6тс в центральном пролете, а так же изгибающий момент 1,89тс*м у крайних опор и -0,27тс*м в центральном пролете.
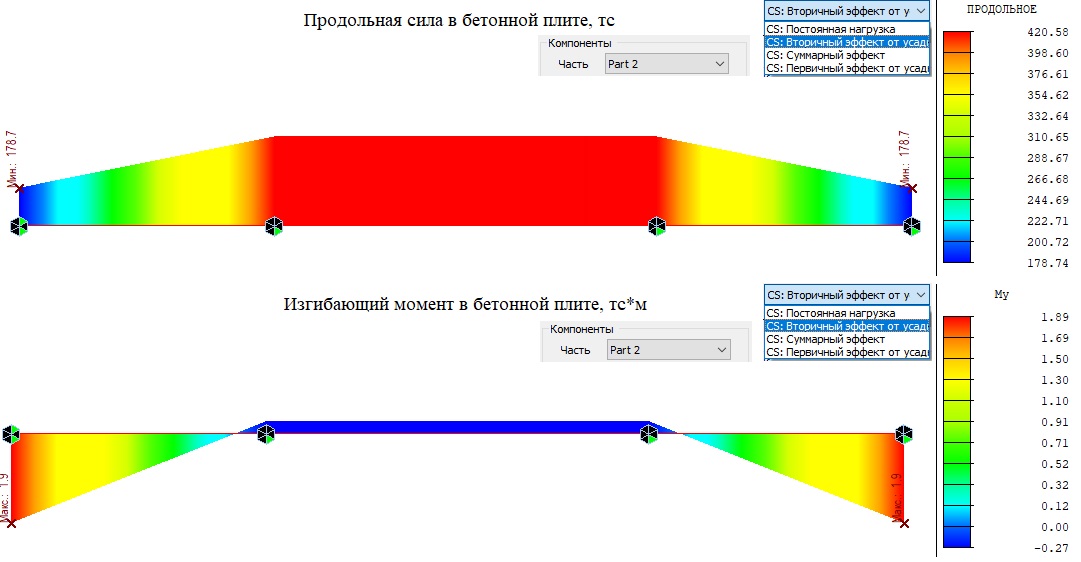
Рисунок 6. Вторичный эффект продольной силы и изгибающего момента в бетонной плите (Часть 2)
Суммарные усилия в СТЖБ балке составят: у крайних опор My = 279+1.9–178.7*1.571662 = 0 тс*м, и в середине пролета My = -39.6–0.27–420*1.571662 = 700 тс*м. Продольные силы в стальной балке и бетонной плите полностью уравновешивают друг друга, поэтому эпюра продольных сил в общем СТЖБ сечении равна нулю. В приведенных расчетах 1,571662 м — расстояние между центрами тяжести стальной и бетонной частей.
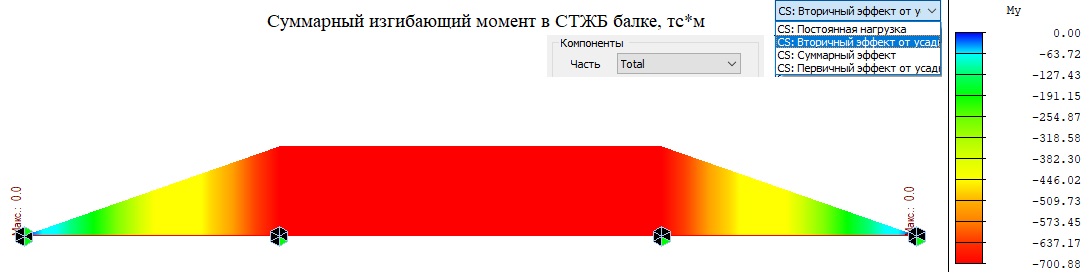
Рисунок 7. Вторичный эффект изгибающего момента в объединенном СТЖБ сечении (Часть «Total»)
Значения опорных реакций от усадки бетона показаны на рисунке 8.

Рисунок 8. Значение суммарных опорных реакций от усадки
Вторая задача с эквивалентной сжимающей силой вместо самой усадки
Попробуем разобраться, как были получены эти деформации и усилия, а также в том, что такое первичный и вторичный эффекты.
Судя по заданной кривой усадки, относительные деформации бетона по итогу 100 лет составят 0.0002. Определим, какую сжимающую силу к бетонной плите необходимо приложить для того, чтобы она укоротилась на эту величину. При модуле упругости Eb=3518000 тс/м2, воспользуемся законом Гука для определения напряжений в бетоне при относительных деформациях 0.0002. σ =ε * Eb = 0.0002 * 3518000 = 703.6тс/м2. Ширина плиты составляет Bc = 6.75 м, а толщина плиты tc = 0.24 м, отсюда площадь равна Ab = Bc * tc = 6.75 * 0.24 = 1.62 м². Умножим напряжения на площадь и получим величину сжимающей продольной силы N = σ * Ab = 703.6 *1.62 = 1140тс. Это та величина продольной силы, которую мы видели на рисунке 4, в первичном эффекте. С точки зрения получения деформаций пролетного строения, все логично.
Определим деформации балки, показанные на рисунке 3, не прибегая к заданию ползучести, а используя только лишь эквивалент этой сжимающей силы. Создадим новую задачу с этим же пролетным строением, но без задания усадки. Данное трехпролетное строение два раза статически неопределимо, поэтому на первом этапе к СТЖБ балке приложим 1140тс сжатия в уровне центра тяжести бетонной плиты, при этом уберем закрепления на обоих промежуточных опорах. Вертикальные перемещения составляют -186.4 мм.

Рисунок 9. Вертикальные деформации пролета длиной 147 м с отсутствующими промежуточными опорами
Так как промежуточные опоры в местах опирания трехпролетной балки не позволяют ей деформироваться, вернем узлы опирания в исходное состояние. Сделать это можно, приложив к ним вертикальные силы, равные по величине значению опорных реакций, показанных на рисунке 8.
В итоге деформации обеих расчетных моделей равны. Сравним рисунки 3 и 9. Таким образом, можно сделать вывод, что для оценки прогибов используются результаты первичного эффекта, то есть от фиктивных усилий сжатия бетонной плиты соответствующих деформациям усадки.
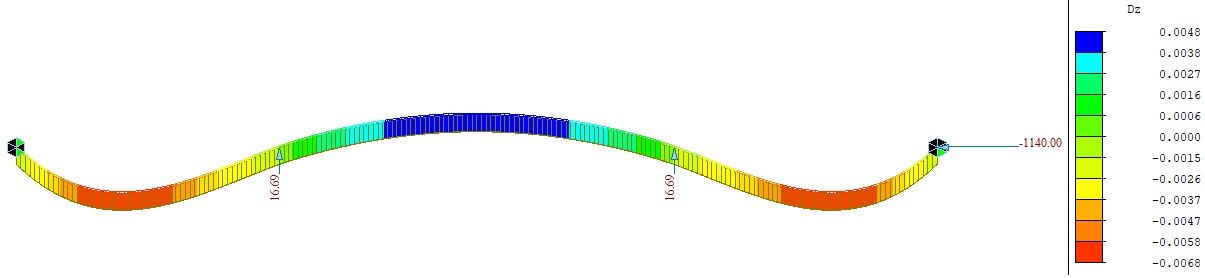
Рисунок 10. Вертикальные деформации от сжатия плиты в статически неопределимой расчетной модели
Третья задача, в которой присутствует усадка, но с разделением внутренних усилий от усадки и от статической неопределимости модели
Подход с приложением эквивалентной сжимающей силы к бетону для получения усилий в элементах составного сечения применять нельзя, так как бетон плиты не испытывает сжатие. В процессе усадки бетон уменьшает свой объем. Укорачиваясь сам, он увлекает за собой стальную балку, тем самым сжимая её. Сам бетон при этом начинает испытывать растяжение, равное создаваемому усилию сжатия стальной балки. За счет наличия эксцентриситета (расстояния между центрами тяжести бетона плиты и стальной балки), в стальной части появляется так же изгибающий момент. Поэтому для получения усилий в частях составных сечений не используется первичный эффект, а используется только вторичный, который включает в себя пересчитанные внутренние усилия в стали и бетоне, исходя из состояния искривления балки, показанной на рисунке 9 (при условии сжатой стали и растянутого бетона), а также дополнительные усилия от раскрытия статической неопределимости задачи.
По аналогии с тем, как мы использовали статически определимую задачу с эквивалентной силой, с последующим заданием опорных реакций от отсутствующих промежуточных опор. Создадим новую модель, в которой уже вместо эквивалентной силы будет задана усадка бетонной плиты, описанная в самом начале статьи. На рисунках 11 и 12 показаны вторичные эффекты — эпюры продольных сил и изгибающих моментов от усадки бетона. Мы видим, что стальная балка сжата от укорочения бетона на 178.74тс, бетонная плита растянута на эту же величину. При этом в стальной балке и бетонной плите появляются также изгибающие моменты величиной 279,03тс*м и 1.89тс*м. Которые в сумме равны продольной силе умноженной на расстояние между центрами тяжести бетонной плиты и стальной балки 178.74 * 1.571662 = 280.92 тс*м.
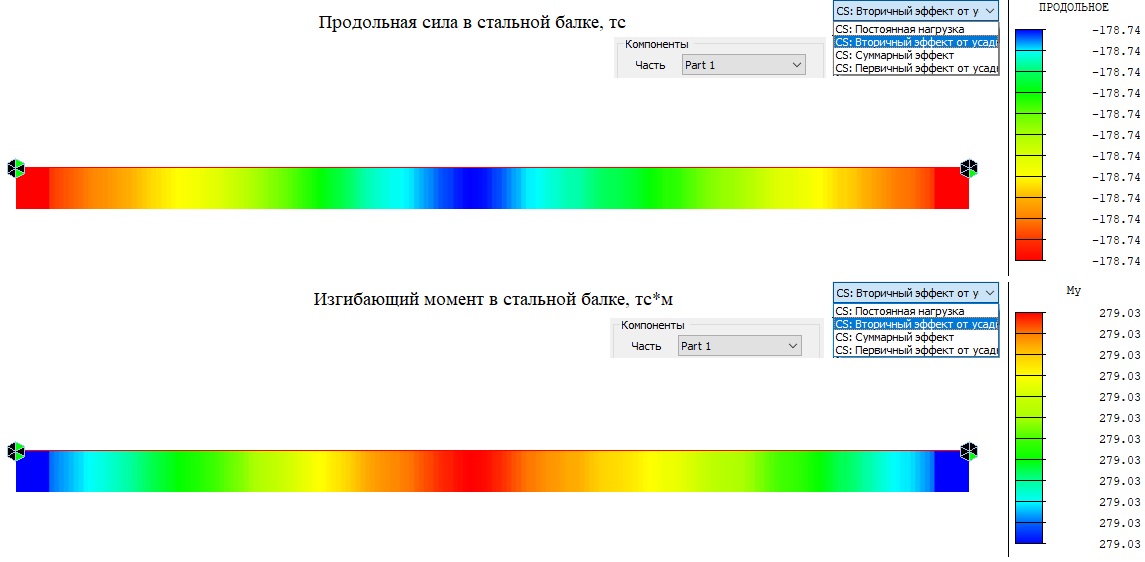
Рисунок 11. Вторичный эффект продольной силы и изгибающего момента в стальной балке (Часть 1). Статически определимая модель.
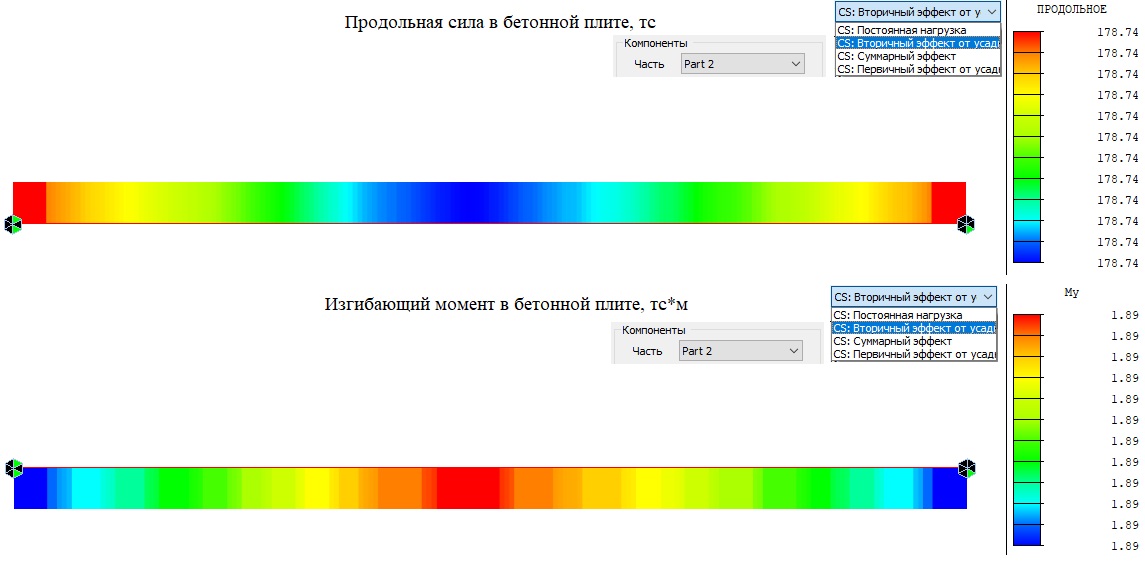
Рисунок 12. Вторичный эффект продольной силы и изгибающего момента в бетонной плите (Часть 2). Статически определимая модель.
Так как все усилия (моменты и продольные силы) в стали и бетоне уравновешивают друг друга, суммарные усилия в общем СТЖБ сечении «Total», в статически определимой задаче равны нулю.
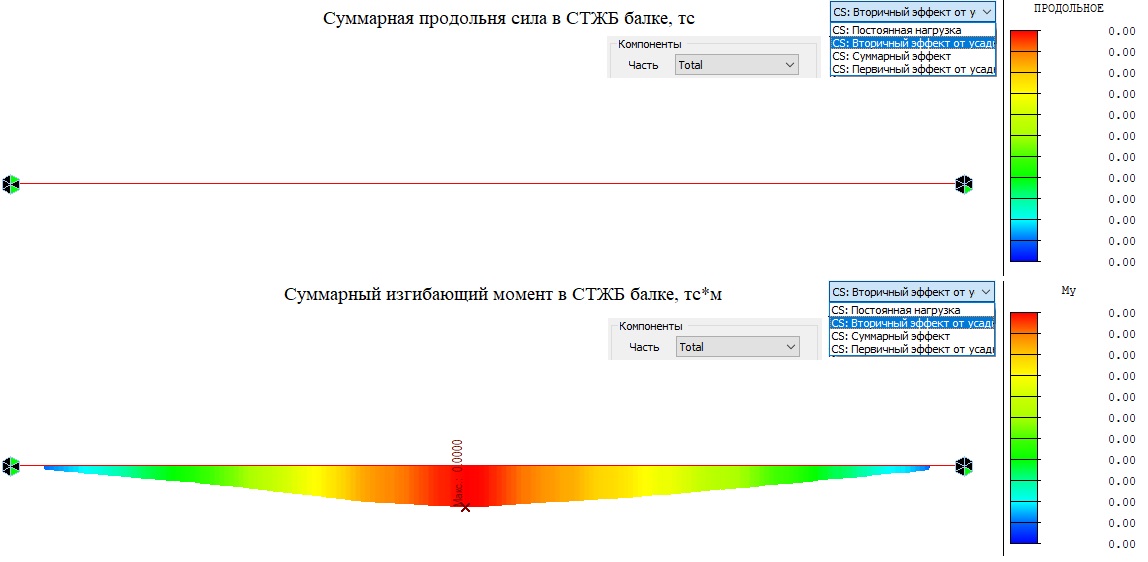
Рисунок 13. Вторичный эффект продольной силы и изгибающего момента в объединенном СТЖБ сечении (Часть «Total»). Статически определимая модель.
Далее получим усилия в бетоне и стали от загружения сосредоточенных сил, равных опорным реакциям, которые возникают в модели со статической неопределимостью от усадки бетона.

Рисунок 14. Эпюры продольной силы и изгибающего момента в стальной балке (Часть 1) от внешних сил равных значению опорных реакций от усадки бетона.

Рисунок 15. Эпюры продольной силы и изгибающего момента в бетонной плите (Часть 2) от внешних сил равных значению опорных реакций от усадки бетона.
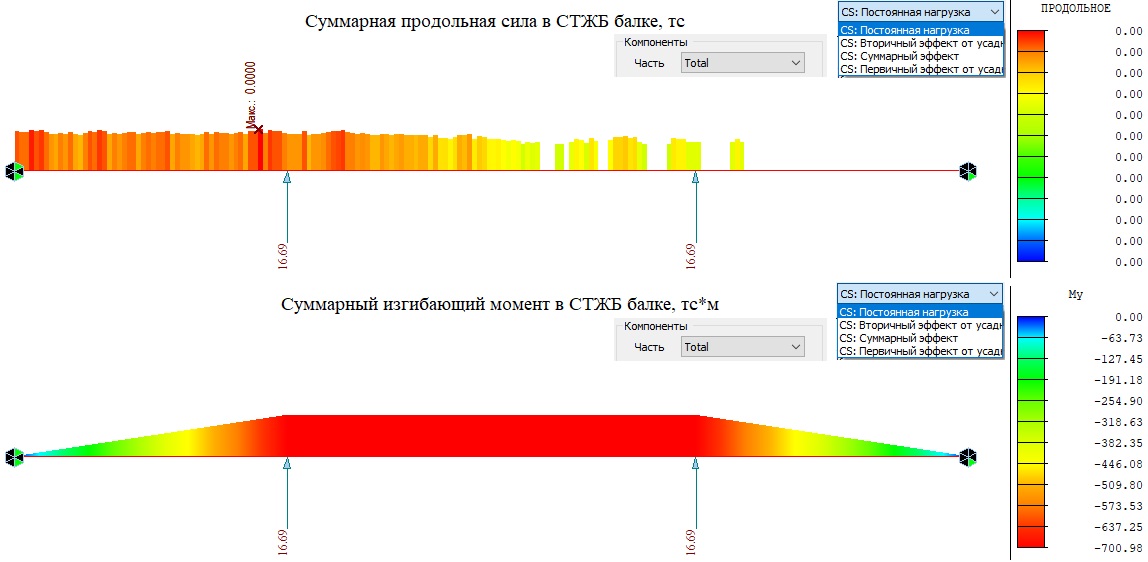
Рисунок 16. Эпюры продольной силы и изгибающего момента в СТЖБ балке (Часть Total) от внешних сил равных значению опорных реакций от усадки бетона.
Просуммировав усилия в стальной и бетонной частях от усадки бетона в статически определимой задаче, с усилиями от раскрытия статической неопределимости модели от этого же явления усадки (Задача 3), мы будем иметь те же усилия, которые получены при расчете статически неопределимой модели от усадки (Задача 1).
Сумма усилий в стальной части (рис. 10 + рис. 13 = рис. 5) Nкрай = -178.74 + 0 = 178.74тс; Mкрай = 279.03 + 0 = 279.03тс*м; Nсер = -178.74 -241.88 = -420.62тс; Mсер = 279.03 — 318.67 = -39.64тс*м;
Сумма усилий в бетонной части (рис. 11 + рис. 14 = рис. 6) Nкрай = 178.74 + 0 = 178.74 тс; Mкрай = 1.89 + 0 = 1.89 тс*м; Nсер = 178.74 + 241.88 = 420.62 тс; Mсер = 1.89 — 2.16 = -0.27 тс*м;
Сумма усилий в бетонной части (рис. 12 + рис. 15 = рис. 7) Nкрай = 0 + 0 = 0 тс; Mкрай = 0 + 0 = 0 тс*м; Nсер = 0 + 0 = 0 тс; Mсер = 0 — 700.98 = -700.98 тс*м; (Mсер = -39.64–0.27–420.62*1.571662 = 700.98 тс*м)
Выводы
- Деформации СТЖБ балки, полученные от усадки бетона, вычисляются через фиктивные усилия сжатия плиты, величина которых определяется из условия достижения плитой заданных относительных деформаций усадки. Данные фиктивные усилия и находятся в первичном эффекте.
- Усилия в стальной балке, бетонной плите и суммарные усилия в объединенном СТЖБ сечении, полученные от усадки бетона, не могут быть определены используя фиктивные усилия,
т. к. фактически бетонная плита во время усадки не испытывает сжатие, а наоборот растянута. Программа внутренне пересчитывает усилия в элементах СТЖБ сечения для получения таких же деформаций конструкции от усадки бетона полученной в первичном эффекте, но с учетом растянутой, а не сжатой плиты. После чего, к полученным усилиям, прибавляются усилия, раскрывающие статическую неопределимость модели. Все эти усилия входят во вторичный эффект. - Опорные реакции. В статически определимой задаче усадка не вызывает появление опорных реакций, так как отсутствуют связи ограничивающие деформации конструкции. Опорные реакции от усадки бетона появляются только в статически неопределимых задачах.
Пройдите бесплатный вводный курс по midas Civil
Создайте модель СТЖБ пешеходного путепровода и выполните линейный расчет двух типов

