Инструмент «Назначение изменения граничных условий», находящийся во вкладке «Расчет», позволяет пользователю задавать для разных нагрузок различные: связи, закрепления, масштабные коэффициенты к жесткостям элементов. Можно даже выполнять различные типы расчетов (статический, динамический, на подвижную нагрузку) с различными граничными условиями в рамках одной модели, не создавая несколько отдельных файлов.

Сегодня мы разберем данную функцию более подробно на двух примерах. В первом примере будет использоваться подвижная нагрузка. Во втором примере рассмотрим использование разных закреплений для статических загружений применительно к нестандартному решению моделирования монтажа пролетного строения методом продольной надвижки без стадийного расчета.

Использование отдельных закреплений при расчете временной нагрузки

Наверное каждый инженер сталкивался с таким явлением, когда, в случае установки нескольких продольно-неподвижных опорных частей на одной из опор, от подвижной нагрузки возникают достаточно большие значения продольных реакций. Это связано с неравномерностью приложения нагрузки относительно продольной оси пролетного строения, что и вызывает разнонаправленные значения продольных опорных реакций в абсолютно жестких закреплениях.

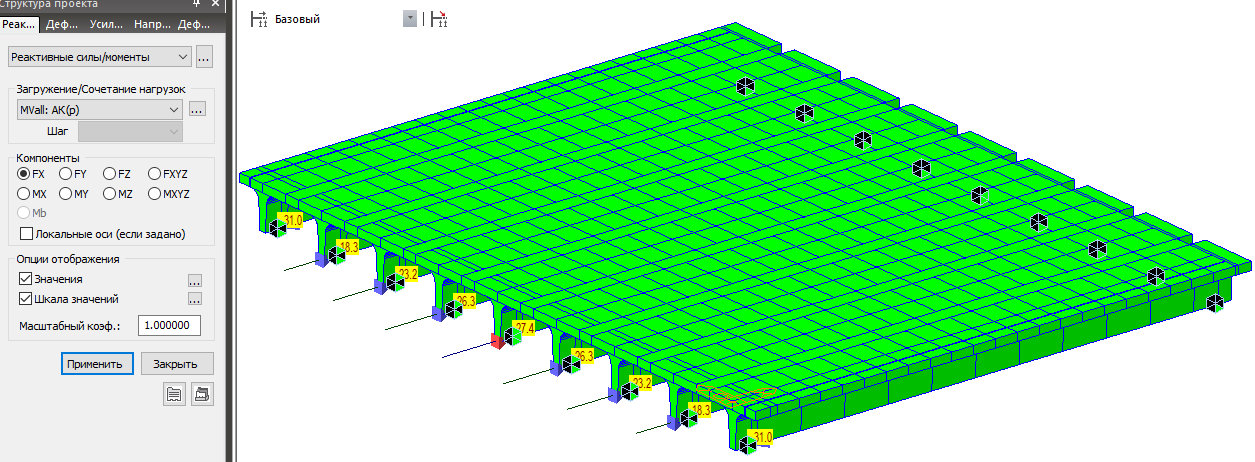
Рисунок 1

Но, так как в природе нет ничего абсолютно жесткого, податливость имеется всегда: зазоры в неподвижных опорных частях, деформация опорных частей и элементов опор (ригелей, стоек) и т. д. Все это позволяет конструкции «дышать» на несколько миллиметров. А этого вполне достаточно для того, чтобы данные реакции практически обнулились. В случае, если инженер не хочет учитывать данные реакции в своих расчетах, он может воспользоваться инструментом «Назначение изменения граничных условий».

Для этого необходимо создать группы граничных условий, в которые нужно добавить необходимые закрепления опорных узлов. В нашем случае группы будет две: «Временная» и «Статический расчет». В группу «Статический расчет» будут добавлены закрепления с учетом ряда продольно-неподвижных ОЧ, а в группы «Временная» войдут закрепления только с одной продольно-неподвижной опорной частью.

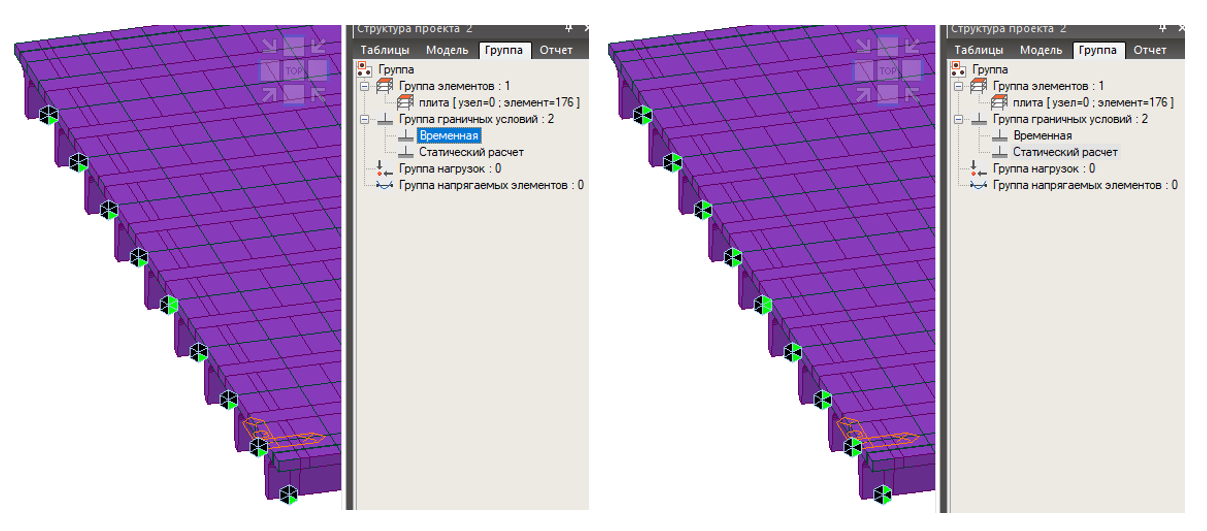
Рисунок 2

Далее в «Назначение изменения граничных условий» нужно создать сочетания граничных условий для данных групп нагрузок. В данном случае в сочетание «Временная» входит группа с таким же названием, а в сочетание «Постоянная» входит группа «Статический расчет». После чего присваиваем всем статическим загружениям сочетание «Постоянная», а подвижным нагрузкам — сочетание «Временная».

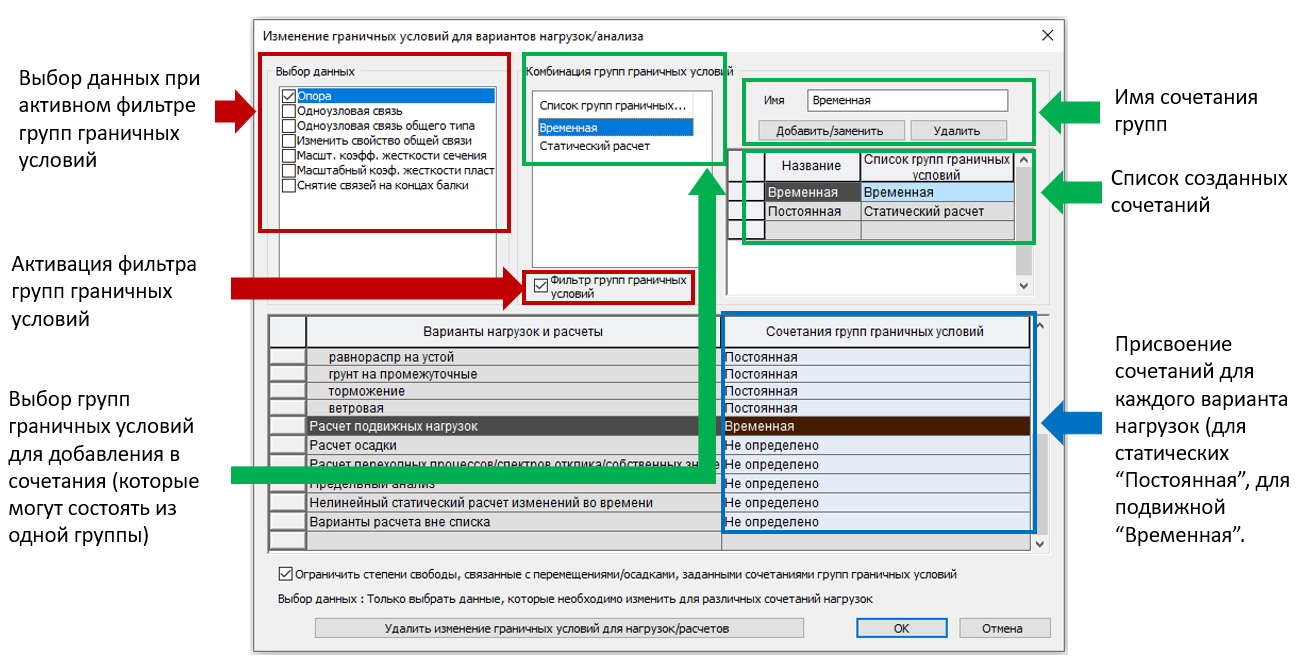
Рисунок 3

После этого можно запускать на расчет.

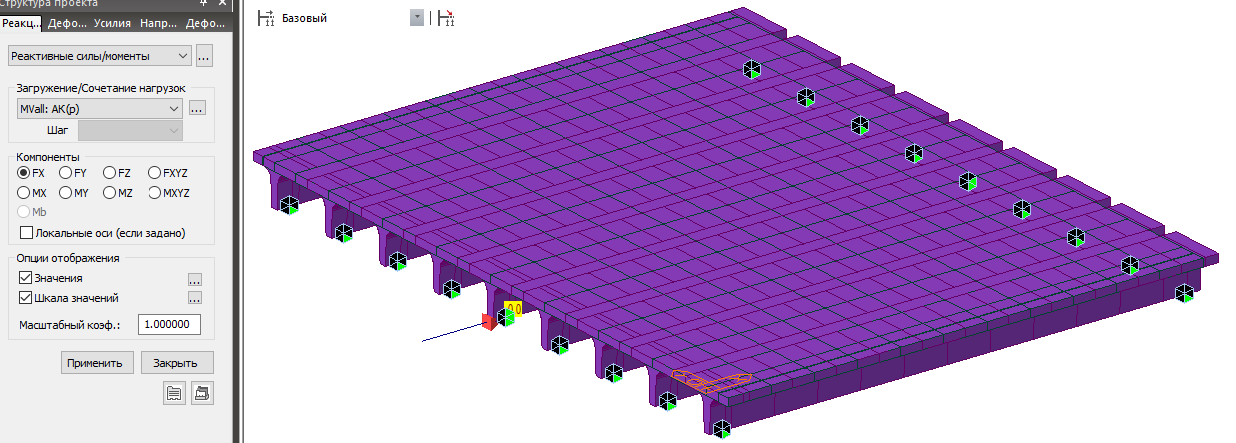
Рисунок 4

В результате мы получим отсутствие продольных реакций на всех опорных частях первой опоры от временной нагрузки. При этом от прочих нагрузок реакции не изменятся.

Если оценить продольные перемещения опорных узлов на первой опоре от временной нагрузки (с отсутствующими продольными связями), то мы увидим, что максимальные значения достигают DX=1.3 мм.

Далее результаты по деформациям узлов, усилиям и напряжениям в элементах, опорным реакциям в закреплениях можно суммировать в сочетаниях и выполнять проверки на эти сочетания.

Использование отдельных закреплений в статических загружениях

Разберем на примере моделирования надвижки. Конечно, данный способ не предполагает поэтапную активацию элементов пролетного строения на стапеле ввиду отсутствия стадийного расчета. По сути все сводится к тому, что, имея большое количество одинаковых загружений постоянной нагрузкой, мы для каждого загружения создадим различные положения мест опирания балки на опоры. Результаты по каждому загружению будут являться этапами надвижки. Так как при таком способе монтажа пролетного строения не происходит накопления усилий, а так же отсутствуют какие-либо реологические процессы и пластические деформации, данный способ вполне допустим.

В нашем примере рассмотрена двутавровая балка. Среди нагрузок только собственный вес. Количество статических загружений данной нагрузкой 12 (равно количеству стадий). Затем добавим в каждый узел балки опорное закрепление, создадим группы граничных условий, равное количество узлов главной балки и распределим каждое закрепление в отдельную группу.

Рисунок 5

Теперь нам осталось в «Назначение изменения граничных условий» собрать из данных групп граничных условия сочетания с закреплениями.

Предположим, что на первой стадии активируются опорные закрепления с номерами групп закреплений 19, 32, 52, 70(замыкающий). Они входят в сочетание «Стадия1», которое присваивается первому загружению собственным весом «СВ». Далее смещаем узлы опирания на один в направлении надвижки, таким образом в сочетание «Стадия2», войдут группы закреплений 20, 33, 53, 70 (замыкающий), плюс на данной стадии край консоли наезжает на следующую опору 1. Сочетание закреплений «Стадия2» присваивается ко второму загружению постоянной нагрузкой «СВ2» и т. д.

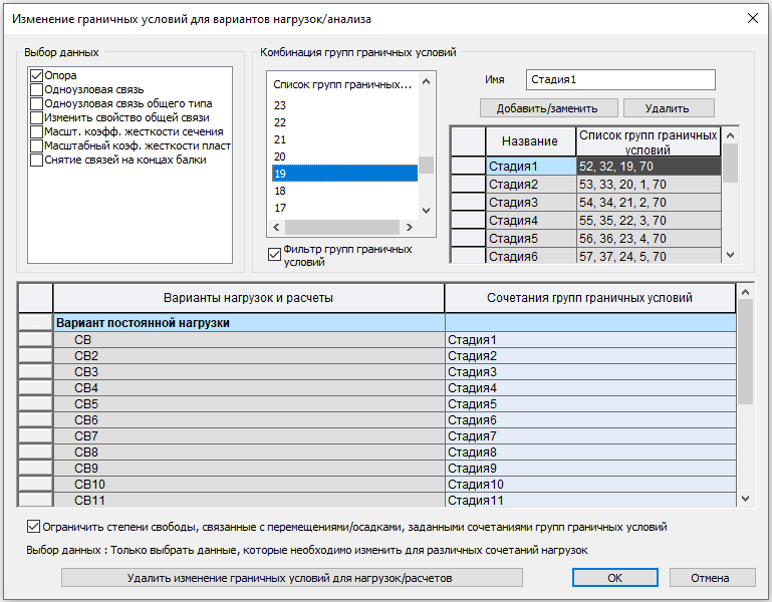
Рисунок 6

Таким образом, мы имеем собственные закрепления для каждой нагрузки, условно разделенные по стадиям. В рамках одной расчетной модели мы посчитаем несколько состояний конструкции. Используя огибающее сочетание среди этих нагрузок, можно получить максимальный или минимальный результат среди всех «стадий».

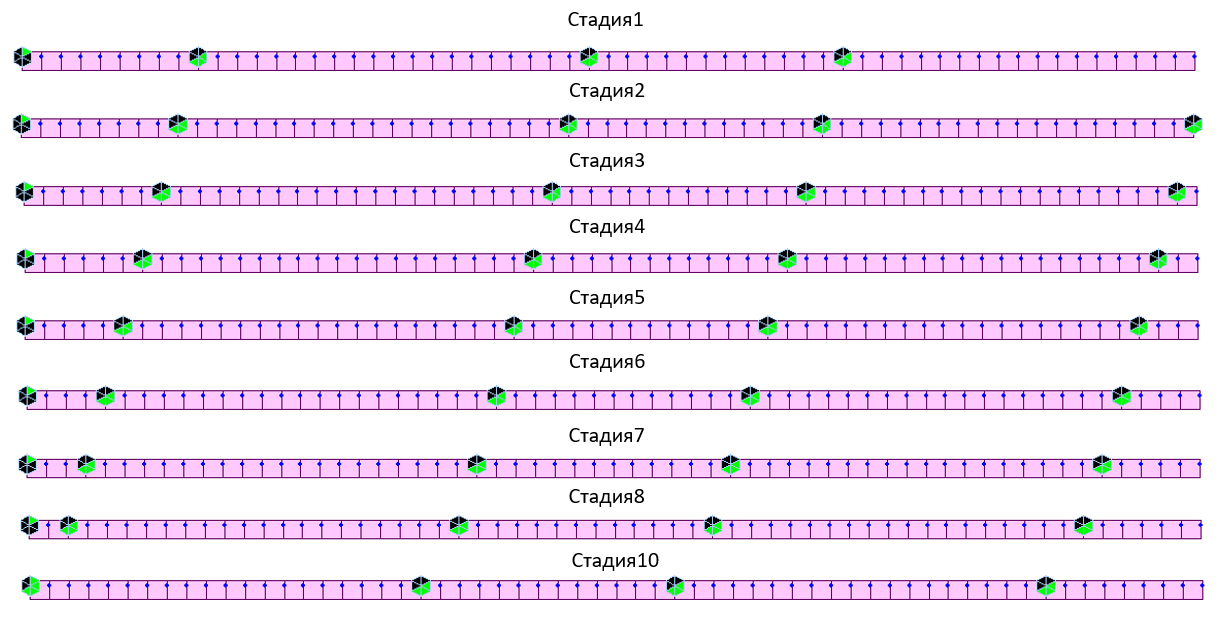
Рисунок 7

Так выглядит эпюра изгибающих моментов по стадиям и огибающая эпюра моментов среди всех стадий.

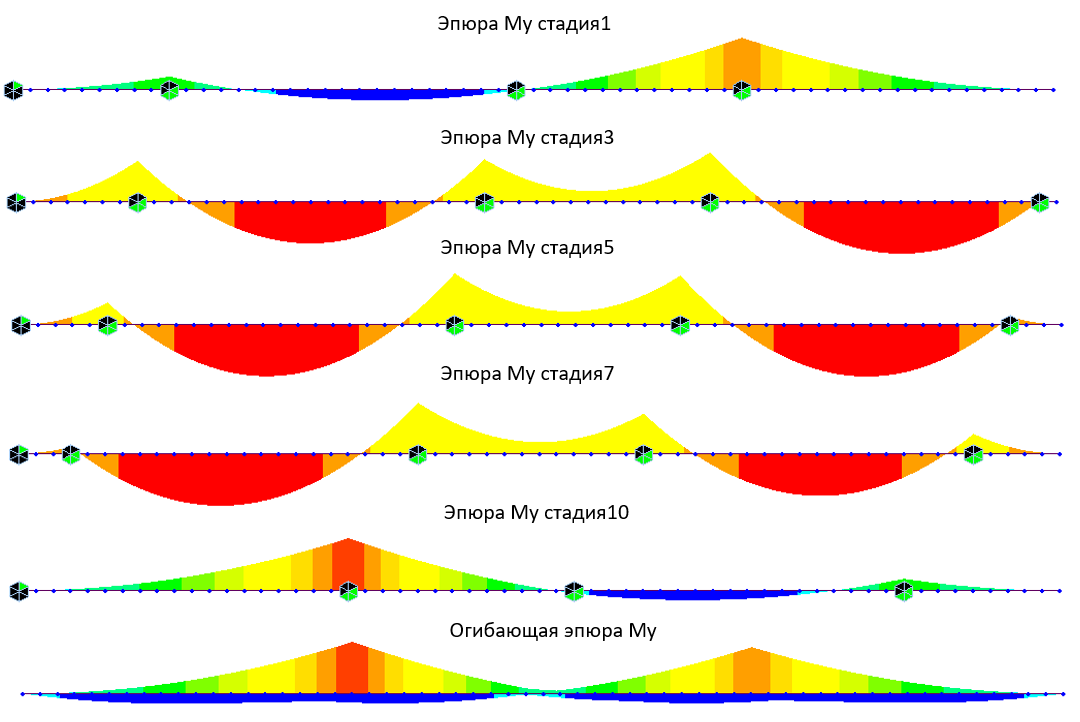
Рисунок 8

Если вас заинтересовала статья, то вы можете получить больше информации в справке midas Civil, которая находится в правом верхнем углу программы. Перейдите в содержание справки и найдите раздел «Управление расчетом» в «Старт» — «Расчет» — «Управление расчетом» — «Изменение граничных условий».